Att hitta yta kottar är inte så svårt. Men det kan kräva lite tålamod och uppfinningsrikedom, beroende på vilken information som finns tillgänglig i början av problemet. Nedan följer några förslag på åtgärder för att hålla reda på allt.
Steg
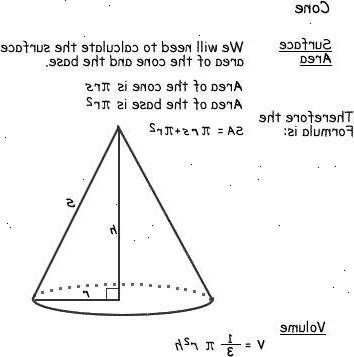
- 1Identifiera radien på konens bascirkel. Om du har diametern, halvera det att få radien. Om du har den lutande höjd och vinkelräta höjden, använd Pythagoras sats (se "Tips" nedan).
- 2Skriv radien någonstans åt sidan, där det är märkt och lätt att hitta, eftersom du kommer att behöva det flera gånger i flera olika beräkningar.
- 3Hitta området bascirkeln genom kvadrering radien och multiplicera med pi.
- Om instruktionerna säger något liknande "exakt värde", betyder det att du skriver den grekiska bokstaven för pi och lämna det. Så en radie av 3 ger en yta på 9pi.
- Annars använder 3.14 eller räknarens pi-knappen för att avsluta multiplikation och få en decimal version för området.
- Du kan avrunda, men hålla minst 3 siffror efter decimalkommat för nu.
- Du kan avrunda, men hålla minst 3 siffror efter decimalkommat för nu.
- Om instruktionerna säger något liknande "exakt värde", betyder det att du skriver den grekiska bokstaven för pi och lämna det. Så en radie av 3 ger en yta på 9pi.
- 4Skriv att svara på ena sidan, någonstans där det är märkt "basområde" och lätt att hitta.
- 5Identifiera lutande höjden av konen. Detta avser höjden längs den lutande sidan av könen, inte höjden från spetsen av könen till centrum av cirkeln.
- Radien, den vinkelräta höjden (från spets till centrum), och lutande höjd är relaterade med Pythagoras sats. Se "tips" nedan.
- Radien, den vinkelräta höjden (från spets till centrum), och lutande höjd är relaterade med Pythagoras sats. Se "tips" nedan.
- 6Multiplicera livets lutande höjd gånger radien gånger pi. Återigen, "exakt värde" betyder write pi som pi, annars använd 3.14 för att få närmevärde.
- 7Skriv att svara på ena sidan, någonstans där det är märkt "sidoområde" och lätt att hitta.
- 8Lägg till "base området" från steg 4 med "sidoområde" från steg 7.
- 9Rund, vid behov. Detta är ditt slutgiltiga svar.
Tips
- Pythagoras sats gäller radien, vinkelräta höjd, och lutande höjd, med lutande höjd fungerar som hypotenusan: (radie) 2 + (vinkelräta höjd) 2 = (lutande höjd) 2
- Allmänna avrundningsregler: något svar under 20 behöver minst 2 decimaler. Varje svar mellan 20 och 100 behöver endast en decimal. Något svar över 100 kan avrundas till närmaste heltal.
Varningar
- Om antingen din radie eller din lutande höjd har en kvadratrot, kommer du inte att kunna avsluta tillsats på steg 8.
