Bestämmelse av matriser är mycket användbara och som krävs för att hitta inversen av en matris för hand samt för att tillämpa vissa ekvationslösning processer såsom Cramers regel. Dessutom, om determinanten är 0, vet du de ekvationer som utgör din matris är linjärt beroende.
Steg
- 1Låt M vara 3x3 matris och dess determinant blir | m |.
Exempel:en 11 en 12 en 13 1 5 3 M = en 21 en 22 en 23 = 2 4 7 en 31 en 32 en 33 4 6 2 - 2Ta en referens rad eller kolumn. Med en referens rad eller kolumn i detta problem är ett avgörande steg som om du väljer klokt, så du kan lindra problemet mycket och lösa problemet på mycket kortare tid.
- Generellt första raden tas som referens. Om den givna matrisen har noll i sina beståndsdelar och sedan välja Reference rad eller kolumn, som har flest nollor.
- Det är ett tecken avtal för referens rad eller kolumn enligt vilken man måste göra beräkningen. Observera att detta teckenkonvention endast för referens rad eller kolumn. Den teckenkonvention ges nedan.
(+) A 11 (-) A 12 (+) En 13 M = (-) A 21 (+) A 22 (-) A 23 (+) A 31 (-) A 32 (+) En 33
- Generellt första raden tas som referens. Om den givna matrisen har noll i sina beståndsdelar och sedan välja Reference rad eller kolumn, som har flest nollor.
- 3Välj det första elementet från referens rad eller kolumn och stryka andra element från den rad och kolumn är markerat element i.
- Beräkna determinanten av 2X2 matris som är kvar efter att ha passerat ut element i steget ovan. Sedan multiplicera 2X2 determinant med valda referens elementet och motsvarande tecken för att hänvisningen elementet.
- Om du tar första raden som referens, då för det första elementet:
(+) En 11 * ((a 22 * a 33) - (en 23 * 32)) = 1 (4 * 2 - 7 * 6) = -34
- Beräkna determinanten av 2X2 matris som är kvar efter att ha passerat ut element i steget ovan. Sedan multiplicera 2X2 determinant med valda referens elementet och motsvarande tecken för att hänvisningen elementet.
- 4Välj det andra elementet från referens rad eller kolumn och stryka andra element från den rad och kolumn är markerat element i.
- Beräkna determinanten av 2X2 matris som är kvar efter att ha passerat ut element i steget ovan. Sedan multiplicera 2X2 determinant med valda referens elementet och motsvarande tecken för att hänvisningen elementet.
- Om du tar första raden som referens, sedan för det andra elementet:
(-) 12 * ((a 21 * a 33) - (a 23 * a 31)) = (-) 5 (2 * 2 - 7 * 4) = 120
- Beräkna determinanten av 2X2 matris som är kvar efter att ha passerat ut element i steget ovan. Sedan multiplicera 2X2 determinant med valda referens elementet och motsvarande tecken för att hänvisningen elementet.
- 5Välj den tredje elementet från referens rad eller kolumn och stryka andra element från den rad och kolumn är markerat element i.
- Beräkna determinanten av 2X2 matris som är kvar efter att ha passerat ut element i steget ovan. Sedan multiplicera 2X2 determinant med valda referens elementet och motsvarande tecken för att hänvisningen elementet.
- Om du tar första raden som referens, då för det tredje elementet:
(+) En 13 * ((en 21 * 32) - (a 22 * a 31)) = 3 (2 * 6 - 4 * 4) = -12
- Beräkna determinanten av 2X2 matris som är kvar efter att ha passerat ut element i steget ovan. Sedan multiplicera 2X2 determinant med valda referens elementet och motsvarande tecken för att hänvisningen elementet.
- 6Lägg resultaten för tre delar av referens rad eller kolumn för att få faktorn för att 3x3 matris.
| M | = -34 + 120-12 = 74
Tips
- Om alla element i en rad eller kolumn i en matris är noll, så avgörande för denna artikel är också noll.
- Om du tar första raden som referens, då avgörande kommer att vara:
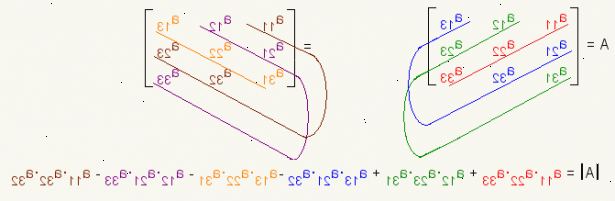
| M | = a 11 * ((a 22 * a 33) - (en 23 * 32)) - en 12 * ((a 21 * a 33) - (a 23 * a 31)) + en 13 * ( (en 21 * 32) - (a 22 * a 31)) - Denna metod omfattar kvadratiska matriser av alla storlekar.
Varningar
- Försök att undvika att göra bestämningsfaktorer för något större än en 3x3 för hand.
