Hur lösa kvadratiska ojämlikheter

1. 1
   Steg 1. Förvandla ojämlikhet i ett trinomialpantheraen f (x) på vänster sida och lämnar 0 på höger sida.
   • Exempel. Den olikhet: x (6 x + 1) <15 kommer att omvandlas till en trinomialpantheraen i x: f (x) = 6 x ² + x - 15 <0.
2. 2
   Steg 2. Lös den kvadratiska ekvationen att få de verkliga rötterna. Du kan använda någon av dessa metoder. I allmänhet kan en kvadratisk ha noll, en eller två reella rötter.
   • Använd kvadratiska formel (fungerar alltid)
   • Factoring (om rötterna är rationella)
   • Kvadratkomplettering (fungerar alltid)
   • Grafritande (approximation)
   • Diagonal summan metod (genväg för factoring). Att veta hur man använder den nya Diagonal Sum Method, läs artikel med rubriken: "Hur löser andragradsekvationer genom Diagonal Sum Method" på denna Googles webbplats.
3. 3
   Steg 3. Lös den kvadratiska ojämlikhet, baserat på värdena för de två reella rötter.
   • Du kan välja en av följande två metoder:
     • Metod 1: Använda tallinjen och provpunkt metod. De två reella rötter ritas på ett antal linje. De delade linjen i ett segment och två strålar. Använd alltid origo O som mätpunkt. Ersätt x = 0 i den givna kvadratiska olikhet. Om det är sant, då origo är beläget på den sanna segment (eller den sanna ray).
     • Obs. Genom denna metod kan du använda en dubbel rad-line, eller ens en trippel rad-line, för att lösa system av 2 eller 3 kvadratiska ojämlikheter i en variabel.
     • Metod 2. Använda en sats på Sign av f (x) om algebraiska metoden väljs. Studenter studerar när satsen utveckling sedan tillämpa den på att lösa olika kvadratiska ojämlikheter.
       • Sats på Sign av f (x):
         • Mellan 2 reella rötter, har f (x) motsatt tecken på en. Det innebär:
         • Mellan de två reella rötter, är f (x) positivt om a är negativt
         • Mellan de två reella rötter, är f (x) negativ om a är positiv.
         • Du kan förstå denna sats genom att titta i skärningspunkterna mellan parabeln grafen av funktionen f (x) och x-axeln. Om a är positivt, är parabel uppåt. Mellan de två x-axeln, är en del av parabeln under x-axeln, dvs f (x) är negativ i detta intervall (omvänt tecken a).
         • Denna metod kan vara snabbare än antalet linje metod, eftersom den inte kräver att dra antalet linje varje gång. Dessutom hjälper det att inrätta en Logga tabell för att lösa system av kvadratiska ojämlikheter som den algebraiska metoden.
4. 4
   Steg 4. Uttryck svaret (eller lösning-set) i form av intervaller.
   • Exempel på intervaller:
   • (A, b),, öppet intervall de 2 sista punkterna a och b inte är inkluderade
   • [A, b], slutna intervall, är de två ändpunkterna inkluderade
   • (-Oändligheten, b],, halvt slutna intervall är slutpunkten b ingår.
     • Not 1. Om den kvadratiska ekvationen saknar reella rötter, (Diskriminantanalys D <0), är f (x) alltid positiv (eller alltid negativ) beroende på vilket tecken en mening om att den lösning som antingen kommer att vara tom eller hela reella tal linje. Om diskriminanten lika med noll (dvs. det kvadratiska har en dubbel rot), varefter lösningen kan vara tom, en enda punkt, alla reals utom en enda punkt, eller alla reals.
   • Exempel: lösa f (x) = 15x ^ 2 - 8x + 7> 0.
   • Lösning. Diskriminantanalys D = b ^ 2 - 4ac = 64-420 <0. Det finns inga reella rötter. Eftersom a är positivt, är f (x) alltid positiv (> 0) oberoende av värdena på x. Ojämlikheten är alltid sant.
   • Exempel. Lös f (x) =-4x ^ 2 - 9x - 7> 0.
   • Lösning. Diskriminantanalys D = 81 till 112 <0. Det finns inga reella rötter. Eftersom a är negativt, är f (x) alltid negativt, oavsett värdena på x. Ojämlikheten är alltid inte sant.
     • Not 2. När ojämlikheten har ytterligare lika (=) tecknet (större eller lika med, mindre eller lika med), använd slutna intervall som [-4,10] för att indikera att de två ändpunkterna ingår i lösningen set. Om ojämlikhet har strikt större än eller strikt mindre än, använder öppna intervall som (-4, 10) som ändpunkterna inte ingår.

Exempel 1

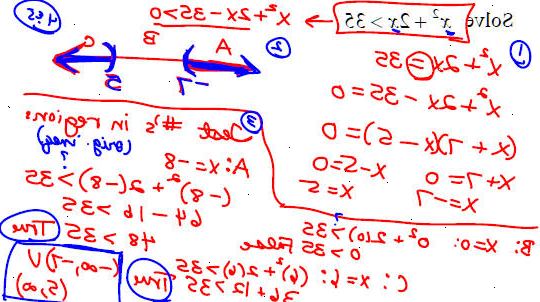
1. 1
   Lös: 15> 6 x ² + 43 x.
2. 2
   Förvandla ojämlikhet i ett trinomialpantheraen i x. f (x) = -6 x ² - 43 x + 15> 0.
3. 3
   Lös f (x) = 0 med hjälp av diagonala summan metoden.
   • Rule of tecken säger de 2 rötterna har motsatta tecken eftersom den konstanta termen och koefficienten för x ² har motsatta tecken.
   • Skriv ner sannolika rötter-set: {-3/2, 5/3}, {-1 / 2, 15/3}, {-1 / 3, 15/2}. Produkten av de täljare är den konstanta termen (15) och produkten av den nämnare är koefficienten för x ² term: 6 (nämnare alltid positiva).
   • Beräkna den diagonala summan av varje kandidat för root par genom att lägga de första täljare gånger den andra nämnaren till den första nämnaren gånger den andra täljare. För detta exempel, de diagonala summorna är (-3) * (3) + (2) * (5) = 1, (-1) * (3) + (2) * (15) = 27, och (-1 ) * (2) + (3) * (15) = 43. Eftersom den diagonala summan av de verkliga rötterna måste vara lika med - b * sign (a) där b är koefficienten för x och a är koefficienten för x ^2, vi vill ha den tredje set, men måste förneka båda lösningarna. De två reella rötter är: {1/3, -15/2}
4. 4
   Använd satsen att lösa ojämlikhet. Mellan de två reella rötter
   • f (x) är positivt, omvänt tecken a = -6. Utanför detta intervall, är f (x) negativ. Eftersom den ursprungliga ojämlikheten hade strikt olikhet, använd öppet intervall för att utesluta ändpunkterna där f (x) = 0.
     • Lösningen uppsättningen är intervallet (-15 / 2, 1/3).

Exempel 2

1. 1
   Lös: x (6x +1) <15.
2. 2
   Förvandla ojämlikhet i: f (x) = 6x ^ 2 + x - 15 <0.
3. 3
   De två rötterna har motsatta tecken.
4. 4
   Skriv ner sannolika rötter-set: (-3 / 2, 5/3) (-3 / 3, 5/2).
   • Den diagonala summan av första set till 10 - 9 = 1 = b.
   • De två reella rötter är 3/2 respektive -5 / 3.
5. 5
   Välj antal-line metod för att lösa ojämlikhet.
6. 6
   Välj som test-punkten origo O. Suppleant x = 0 till ojämlikhet. Den visar: - 15 <0. Det är sant!. Ursprunget är belägen på den sanna segmentet och lösningen uppsättningen är intervallet (-5 / 3, 3/2).
7. 7
   Metod 3. Lösa kvadratiska ojämlikheter genom att rita grafer.
   • Begreppet denna grafritningsmetod är enkel. När parabeln grafen av funktionen f (x) är ovanför x-axeln, då trinomialpantheraen är positiv och vice versa. För att lösa kvadratiska ojämlikheter, behöver du inte att exakt plotta parabel. Baserat på 2 reella rötter, kan du skissa ungefär parabel. Bara vara säker på att parabolen korrekt böjd uppåt eller nedåt.
   • Med denna metod kan man lösa system av två eller tre kvadratiska ojämlikheter genom plottning 2 eller 3 parabler på samma koordinatsystem.