Trigonometri är den gren av matematiken som behandlar studera trianglar. Det är mycket lätt att förstå om närmade sig på rätt sätt. Denna artikel kommer att hjälpa dig att komma igång att lära trigonometri.
Steg
- 1Fräscha upp dina grundläggande matematiska färdigheter. Dessa inkluderar kunskap om algebra och algebraisk manipulation samt geometri.
- Öva algebraisk manipulation. Algebraiska manipulation är en mycket grundläggande färdighet som är nödvändig för att studera någon gren av matematiken.
- Lär dig att ändra ämnet för varje ekvation.
- Lär dig att lösa linjära och kvadratiska ekvationer.
- Lär dig att lösa simultana linjära ekvationer och linjära / kvadratiska par av samtidiga ekvationer.
- Lär dig grundläggande geometri. Geometri är mycket nära släkt med trigonometri och spelar en viktig roll i att lösa trigonometriska problem.
- Lär egenskaperna för en cirkel.
- Lär egenskaper interiören och vinklar utsidan av polygoner inklusive trianglar.
- Lär dig de tre olika typer av trianglar dvs likbent, liksidig och oliksidig.
- 2Börja med att studera rätvinkliga trianglar. Rätvinkliga trianglar är lätta att studera och kommer att ge dig ett bra grepp om grundläggande trigonometri och de tre trigonometriska förhållandena.
- Bekanta dig med de tre sidorna i en rätvinklig triangel.
- Hypotenusan är sidan mitt emot den räta vinkeln. Det är den största sidan av varje rätvinklig triangel.
- De två andra sidorna kallas benen i triangeln. Om du väljer valfri vinkel i triangeln (förutom rätt vinkel), kommer du att se att ett ben är intill vinkeln, och det andra benet är motsatt angränsande> vinkeln.
- Bekanta dig med de tre trigonometriska förhållandena, basen av trigonometri:
- Sinus för vilken vinkel som helst är förhållandet mellan längden av den sida som är motsatt den till längden på hypotenusan.
- Cosinus för vilken vinkel som helst är förhållandet mellan längden på den sida som gränsar till det till längden på hypotenusan.
- Tangenten till vilken vinkel som helst är förhållandet mellan sinus för vinkeln mot cosinus för vinkeln. Det är ofta också tas som förhållandet mellan motstående till den intilliggande. Den första definitionen är speciellt till hjälp för att lösa trigonometriska ekvationer och bevisa identiteter medan andra är tillräckligt för en grundläggande studie av trigonometri.
- 3Flytta den till icke-rätvinkliga trianglar.. Eftersom icke-rätvinkliga trianglar har inte en rät vinkel (det är ungefär definitionen), de tre trigonometriska förhållandena spelar en mindre roll (även om de kan också användas i vissa situationer). Snarare två andra regler blir mycket viktigt: Sinus regeln, och cosinus regeln. Följande artiklar förklara dessa regler i detalj.
- 4Lär dig att mäta vinklar i radianer. Radianer är ett alternativ till grader som ett sätt att mäta vinklar. År 180 o finns pi, eller cirka 3.142, radianer. Radianer är särskilt användbara när det gäller att undersöka egenskaperna hos en cirkel, och används också i fysik vid studiet av vågor och enkel harmonisk rörelse.
- 5Lär dig de övriga tre trigonometriska nyckeltal. Det finns ytterligare tre trigonometriska nyckeltal:
- Cosekant. Det är det reciproka värdet av sinus dvs 1/sin kallas 'COSEC "eller" CSC ".
- Sekant. Det är det reciproka värdet av cosinus kallas "sec".
- Cotangens. Det är den reciproka tangenten kallas "barnsäng".
- 6Öva att lösa trigonometriska ekvationer. Trigonometriska ekvationer är (du gissade rätt) ekvationer involverar trigonometriska funktioner. Trigonometriska ekvationer kan oftast lösas genom att manipulera ekvationen att innehålla endast en trigonometrisk förhållande. Följande metoder används för att omvandla en ekvation som innehåller mer än en trigonometrisk ranson i en ekvation som innehåller endast en:
- Dividera hela ekvationen med en trigonometrisk sikt. Till exempel, om en ekvation har en term i sine liksom en term i cosinus, dela hela ekvationen med cosinus. Uttrycket i sine blir en term i solbränna, och termen i cosinus blir 1. Således har du en ekvation som endast innehåller solbränna.
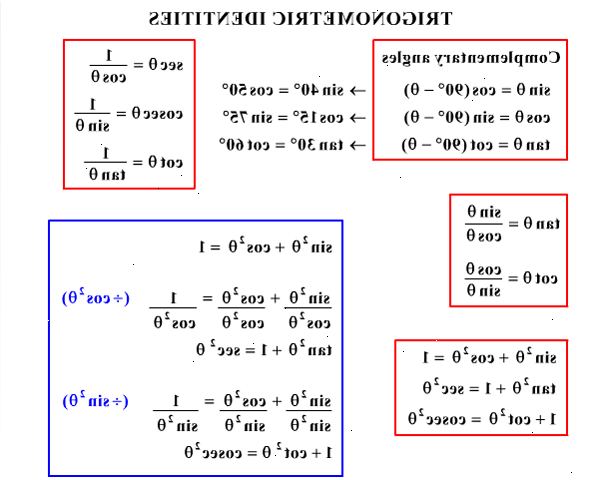
- Med hjälp av en trigonometrisk identitet. Trigonometriska identiteter är "ekvationer" som alltid är sant. Två trigonometriska identiteter skrivs nedan:
sin 2 x + cos 2 x = 1
1 + tan 2 x = sek 2 x.
Alltså, om du hade en ekvation som innehåller en term i sine 2 x och en i cosx, skulle du ersätta termen i sinus 2 x med 1 - cos 2 x från den första identiteten ovan. Det skulle resultera i en kvadratisk i cosx, vilket du bör veta hur man löser (säger så i första steget).
- Bekanta dig med de tre sidorna i en rätvinklig triangel.
- Öva algebraisk manipulation. Algebraiska manipulation är en mycket grundläggande färdighet som är nödvändig för att studera någon gren av matematiken.
Tips
- Du behöver en vetenskaplig kalkylator.
- Titta på svarsknappen om du har fastnat.
- Om du har problem, be en lärare eller en bra elev.
- Granska algebra och geometri, speciellt om du är svag.
- Köp en gradskiva.
- Kom ihåg att matematik är ett sätt att tänka, inte en massa formler för att lära sig. Utveckla dina idéer och vässa dina tänkande genom att lösa problem.
