Hur man lägger till eller subtrahera vektorer

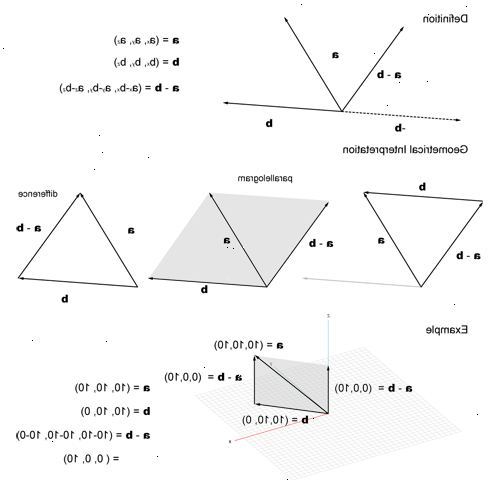
Vektor addition eller subtraktion steg

1. 1
   Om vi har två vektorer, vektor A och vektor B,
   • A = <a1,b1,c1>
   • B = <a2,b2,c2>
2. 2
   Om vi vill lägga vektor A till vektor B, då
   • A + b = <a1+a2,b1+b2,c1+c2>
3. 3
   Om vi vill subtrahera vektorn A från vektor B, då
   • Ab = <a1-a2,b1-b2,c1-c2>

Metod ett: huvud till svans

1. 1
   Ta vilken vektor, och identifiera dess huvud och svansen. Du kan göra en skalenlig ritning, eller en grov skiss. Om du gör en skalenlig ritning, måste du ta hand om konstruera alla vinklar mycket noggrant.
2. 2
   Skjut annan vektor så att svansen ansluter till den första huvud
3. 3
   Gå med alla andra vektorer senare. Ordern spelar ingen roll alls, och denna metod kan användas för något antal vektorer. De bör emellertid vara orienterad så att de börjar bilda en polygon.
4. 4
   Gå med svansen på den första vektorn till chefen för den sista. Detta är den resulterande vektorn, eller summan av alla dina vektorer.
   • Om du ritade diagrammet till en skala, att dra alla vinklar exakt, kan du mäta längden på den resulterande vektorn med hjälp av en linjal. Också då mäta vinkeln att det resulterande gör med antingen en specificerad vektor, eller den horisontella / vertikala etc.
   • Om du skulle göra en skiss, måste du räkna ut storleken på den resulterande använda trigonometri. Du kan hitta och hjälpsamma här. Om du lägger till fler än två vektorer tillsammans, är det bra att först lägga två, och sedan använda den erhållna med den tredje vektorn, och så vidare.
5. 5
   Föreställ din resulterande vektor. Till exempel, om vektorerna representerade hastigheter, sedan skriva "en hastighet av x ms ^-1 vid y ^o till horisontellt / vertikalt / etc".

Metod två: vinkelräta komponenter

Denna metod används vanligen i det kartesiska plan, men kan användas för andra vektorer också.

1. 1
   Split varje vektor i två vinkelräta komponenter. Till exempel, dela varje vektor i sina horisontella och vertikala komponenter. Det är vanligt att dela vektorer i komponenter längs x-, och y-axeln i det kartesiska planet. Den enhetsvektor längs x-axeln är konventionellt skrivet som i, att längs y-axeln som j..
   • För att lösa en kraft i komponenter, måste du veta den vinkel som det gör med den horisontella, vertikala, x-axeln eller y-axeln. När denna vinkel är känd, kan man konstruera en rätvinklig triangel med den kraft som hypotenusan och de två andra sidorna längs x-och y-axlarna. Längderna av de två andra sidorna är storlekarna hos komponenterna längs dessa riktningar, och kan beräknas med hjälp av trigonometri. Den sida intill vinkeln är xcos (vinkel), och den motsatta sidan är xsin (vinkel), där x är storleken på den ursprungliga kraften.
   • Om en komponent pekar åt vänster eller nedåt, får den ett minustecken (-).
2. 2
   Lägg alla storlekarna av de horisontella komponenterna (eller dem längs x-axeln) tillsammans. Separat, lägga till alla storlekarna av de vertikala komponenterna (eller de längs y-axeln). Om en komponent har ett minustecken (-), är dess magnitud subtraheras, snarare än tillsätts.
3. 3
   Beräkna storleken av resultatet med hjälp av Pythagoras sats. Satsen kan anges: c ² = a ² + b ^2, där c är storleken på den resulterande vektorn, a är storleken på summan av komponenter längs med x-axeln, och b är storleken av summan av komponenterna längs y-axeln.
4. 4
   Beräkna vinkel att den resulterande bildar med den horisontella (eller x-axeln). Använd formeln θ = tan ^-1 (b / a), där θ är den vinkel som den resulterande bildar med x-axeln eller den horisontella.
5. 5
   Föreställ din resulterande vektor.
   • Till exempel, om vektorerna representerade krafter, sedan skriva "En kraft x N at y ^o till horisontellt / x-axeln / etc".

Metod tre: vector subtraktion

1. 1
   Subtrahera genom att lägga en negativ. Subtrahera en vektor från en annan kan ses som ett tillägg av dess "negativa".
2. 2
   Hitta den negativa av vektorn. Detta är samma storleksordning som den ursprungliga vektorn, men motsatt i riktning. Du kan representera den genom att göra den ursprungliga vektorn, men dra pilen tvärtom, så att svansen blir huvudet och huvudet blir svansen.
3. 3
   Följ någon tillsats metoden ovan, med det negativa. Använd någon av de två tillägg metoder som beskrivits ovan för att lägga till den "negativa" av vektorn som ska subtraheras och vektorn hade att dras från.