Hur man hittar ett område med en fyrsidig

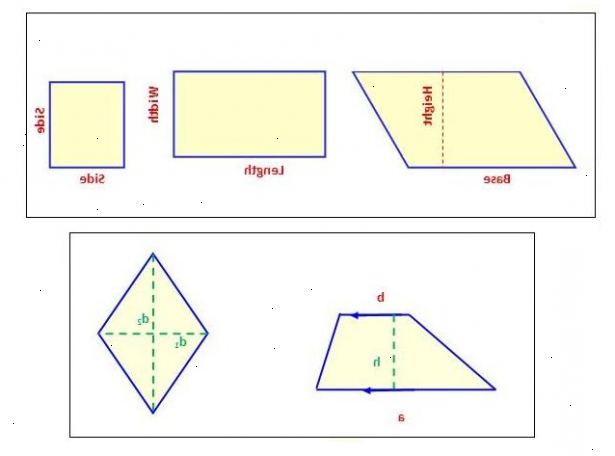
Kvadrater, rektanglar och andra parallellogram

1. 1
   Veta vad en parallellogram är. En parallellogram är en fyrhörning med 2 par parallella sidor, där det motsatta eller vända sidorna är lika långa. Kvadrater, rektanglar och rhombuses är alla parallellogram.
   
2. 2
   Hitta arean av en kvadrat. Eftersom varje sida av en kvadrat är lika långa, kommer du att kvadraten bara längden på ena sidan, kallas t. Använd följande ekvation:
   
   • K = t ²
3. 3
   Hitta arean av en rektangel. För att beräkna arean av en rektangel, behöver du 2 mätningar: bredden, eller bas (den längre sidan av rektangeln), och längden, eller höjden (den kortare sidan av rektangeln). Formeln är:
   
   • K = b * h
4. 4
   Hitta område i en romb (eller diamant). För att hitta ett område med en romb, måste du veta höjden, vilket definieras som det vinkelräta avståndet mellan två parallella sidor. Var försiktig med detta - du kan inte bara multiplicera den ena sidan av en intilliggande sida. Om du behöver hitta höjden av en parallellogram, försöka dra linjen i höjdled så att du har en triangel med en 90-graders vinkel. När du får höjden, använd denna formel:
   
   • K = b * h

Att hitta ett område med en trapets

1. 1
   Veta vad en trapets är. En trapetsformad är en fyrsidig med minst 2 sidor som löper parallellt med varandra. Var och en av fyra sidor på en trapetsoid kan vara en annan längd. Det finns två olika sätt du kan hitta ett område i en trapets, beroende på vilken information du har.
   
2. 2
   Hitta höjden på trapetsen. Höjden på en trapets är vinkelrät linje som förbinder övre baslinje och botten baslinjen, och du kommer att behöva det för både området ekvationer. Detta kommer inte vara samma längd som en av sidorna, eftersom varje sida är riktad diagonalt. Här är hur man hittar höjden:
   
   • Hitta den kortare basen. Placera din penna i hörnet mellan den baslinje och en av sidorna, och dra en linje rakt upp eller ner till den andra baslinjen. Du borde ha skapat en triangel med en 90-graders vinkel.
   • Använd trigonometri för att bestämma höjden. Till exempel, om du vet längden på sidan och att det finns en 90-graders vinkel i triangeln, kan du anta att cosinus för 90 grader kommer att motsvara höjden dividerat med längden på sidan.
3. 3
   Hitta området trapetsen med höjden. Om du känner till höjden på trapetsen, liksom längden på båda baserna, använd följande ekvation:
   
   • K = (a + b) / 2 * h
4. 4
   Hitta område i en parallelltrapets med midsegment. Den midsegment skulle vara en linje som löper parallellt med botten och toppen linjer trapetsen, och bör vara en längd som är precis mellan dem. Här är hur man arbetar med en midsegment:
   
   • Hitta midsegment. För att bestämma midsegment m, ta genomsnittet av sidorna a och b (eller de övre och nedre "baser" av trapetsoiden). Använd denna formel: m = (a + b) / 2. Nu när du vet midsegment, kan du multiplicera det med höjden för att hitta området. Använd följande ekvation:
   • K = m * h

Att hitta ett område med en drake

1. 1
   Veta vad en drake är. En drake definieras som en geometrisk form, i vilken två par av lika långa sidor är intill varandra, som liknar en verklig drake. Det finns två olika sätt att hitta området, beroende på vilken information du har.
   
2. 2
   Hitta det är av en drake använda längderna av sidorna. Om du vet längderna av två olika sidor, samt vinkel i hörnet mellan dessa sidor, använda denna formel i vilken vinkel är theta (θ):
   
   • K = (a * b) * sinö
3. 3
   Hitta område i en kite med diagonaler. En diagonal är den raka linjen mellan två motstående vinklar på draken. Varje drake har 2 diagonaler.
   
   • Bestäm längden av en diagonal. Dra en linje från den ena sidan på draken till en annan. Du bör nu ha två trianglar. Använda, bestämma längden på diagonalen. (Kom ihåg att alla tre vinklarna i en triangel måste lägga upp till 180 grader.)
   • När du har listat ut det första diagonalen, använda samma principer för att bestämma längden på den andra. Använd sedan denna ekvation för att bestämma, där p och q är längden av diagonalerna:
   • K = (p * q) / 2

Använda en allmän ekvation

1. 1
   Använd en allmänt fyrsidigt område ekvation. Det finns formler du kan använda för att räkna ut arean av en fyrsidig, oavsett dess form. Här är de vanligaste som används principerna för trigonometri:
   
   • Om K är den totala arealen av den fyrsidiga, a, b, c och d är längderna av de fyra sidorna, är A den vinkel (i grader) mellan sidorna a och d, och C är vinkeln (i grader) mellan sidorna b och c, då:
     • K = (0.5A * d) * sin A + (0.5b * c) * sin C
     • Om du försöker hitta ett område i en parallellogram, där de motstående vinklar är lika, minskar ekvationen K = 0,5 (ad + bc) * sin A.