Förväntat värde är ett begrepp som används i statistisk analys. Det är ett viktat medelvärde strategi som omfattar multiplicera varje möjligt resultat i ett läge med dess sannolikhet att komma fram till det förväntade resultatet. Det förväntade värdet fungerar som ett genomsnitt, och kan ofta vara en omöjlig utfall i sig, till exempel, är det förväntade värdet av en sex-sidig stansvalsen 3,5. För att beräkna ett förväntat värde, måste du få en förståelse för varje utfall i en situation och dess sannolikhet.
Steg
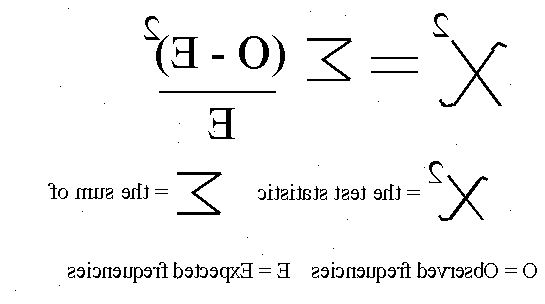
- 1Bekanta dig med den aktuella situationen. Innan räkna upp möjliga utfall och sannolikheter, se till att ha ett samlat grepp om den situation där ett utfall genereras. Till exempel anser en die-rullande spel som kostar 10€ per spel. En 6-sidig tärning slås en gång, och dina kontanta vinster beror på antalet rullade. Rolling en 6 segrar du 25€, rulla en 5 vinner du 15€, rulla något annat nummer resulterar i ingen utbetalning.
- 2Räkna upp alla de möjliga utfall. Det hjälper att göra en lista över alla möjliga utfall i den givna situationen. I exemplet ovan finns det sex möjliga utfall. De är: (1) rulla en 1 och förlorar 10€ (2) rulla en 2 och förlorar 10€ (3) slår en 3 och förlorar 10€ (4) rulla en 4 och förlorar 10€ (5) rulla en 5 och vinna 10€ och (6) slår en 6 och vinna 15€. Observera att 10€ entréavgift subtraheras från varje utfall att komma fram till netto resultatet.
- 3Bestäm sannolikheten för varje utfall. I detta fall är sannolikheten för var och en av de sex resultaten desamma. När rullande en 6-tärningen, är chansen att ett visst nummer som valsas en i sex, eller 16,7 procent. Det är nyttigt att lista dessa sannolikheter bredvid sina resultat, särskilt i fall mer komplicerade än en enkel tärningsslag.
- 4Beräkna det förväntade värdet. Det förväntade värdet beräknas med hjälp av resultaten och deras sannolikheter. Formeln är som följer: O1 * P1 + O2 * P2 + O3 * P3, etcetera. "O" termer representerar de olika utfall, och "P" termer representerar sannolikheten för dessa utfall.
- Fortsätter med exemplet ovan är det förväntade värdet av tärningsspelet: (-10 * 0,167) + (-10 * 0,167) + (-10 * 0,167) + (-10 * 0,167) + (10 * 0,167) + (20 * 0,167), eller - 5€ 0,67. Därför, när du spelar tärningsspel, bör du räkna med att förlora 5€ 0,67 per match.
- 5Förstå innebörden av det förväntade värdet beräkningen. I exemplet ovan, bestämdes det att de förväntade vinsterna i spelet var - 5€ 0,67 per rulle. Detta, naturligtvis, är ett omöjligt resultat i sig, du kan bara antingen förlorar 10€ win 10€ eller vinna 15€. Dock är det förväntade värdet användbar som en långsiktig genomsnittlig siffra. Om du spelar detta tärningsspel om och om igen, kommer du att förlora någonstans nära 5€ 0,67 per match i genomsnitt. Därför är detta spel inte är särskilt gynnsamt för spelaren.
- Ju fler gånger situationen upprepas, desto mer exakt det förväntade värdet kommer att spegla den faktiska genomsnittliga utfallet. Till exempel kan du spela spelet över 5 gånger i rad och förlorar varje gång, vilket resulterar i en genomsnittlig förlust på 10€. Men om du skulle spela spelet 100 gånger eller ännu mer, skulle din genomsnittliga vinster börja reflektera det förväntade värdet mycket prydligt. Denna princip följer av det passande namnet "stora talens lag."
- Den enkla spel ovan illustrerar den princip som spelande fungerar. Den genomsnittliga utbetalningen är negativ, vilket innebär att huset kommer att gynnas av spelet. Däremot lockar tjusningen av en eventuell stor utbetalning spelare till spelet.
Tips
- För situationer där det finns många resultat kan du skapa ett kalkylprogram för att beräkna det förväntade värdet av resultaten och deras sannolikheter.
- Beräkningarna ovan kommer också att arbeta när den uttrycks i andra valutor.
Saker du behöver
- Pencil
- Papper
- Kalkylatorn
