Produkten ögonblick korrelationskoefficienten kan du räkna ut det linjära beroendet av två variabler (kallas x-och y). Ett exempel i ekonomi kan vara att du är ägare av en restaurang. För var 10: e kund du registrera den tid han bodde i din restaurang (x, i minuter) och det belopp som spenderar (y, i dollar). Är det allmänt sant att de långa kvarvarande företagen är också de större spenders? Detta skulle vara en positiv korrelation. Eller är det faktiskt tvärtom, t.ex. rikare kunden desto mindre tid han tar för sin lunch? Detta skulle vara en negativ korrelation. För att sprida lite ljus över detta mysterium kan du beräkna PMCC.
Steg
- 1Ta bort ofullständiga par. I nästa steg använder endast de yttranden där både x och y är kända. Däremot utesluter inte observationer bara för att ett av värdena är lika med noll.
- 2Sammanfatta data till de värden som behövs för beräkningen. Dessa är:
- N - antalet data.
- Sx - summan av alla x-värden.
- Sx 2 - summan av kvadraterna av x-värden.
- Σy - summan av alla y-värdena.
- Σy 2 - summan av kvadraterna av y-värdena.
- Σxy - summan av varje x-värde multiplicerat med dess motsvarande y-värde.
- 3Beräkna s xy, s xx och s yy använda dessa värden.
- S xy = Σxy-(ΣxΣy ÷ n)
- S xx = Sx 2 - (ΣxΣx ÷ n)
- S yy = Σy 2 - (ΣyΣy ÷ n)
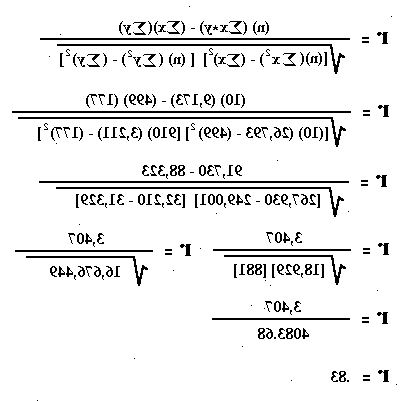
- 4Sätt dessa värden i ekvationen nedan för att beräkna produkten koefficienten ögonblick korrelation (r). Värdet ska ligga mellan 1 och -1.
- Ett värde nära 1 innebär en stark positiv korrelation. (Ju högre x, desto högre y).
Tips
- Alltid göra ett spridningsdiagram. Annars kan du missa din upptäckt eftersom produkten ögonblick korrelationskoefficienten tar bara raka linjer beaktas i branschen för att förutsäga y från x.
- Detta är anledningen till att en hel del enkäter har samma frågor, vilket gör dem oerhört tråkigt att svara. Forskarna vet ofta mycket om fråga x och y fråga, men de vet inte ännu hur de är relaterade.
Varningar
- Innan du ange att två variabler är korrelerade se korrelationskoefficienten är statistiskt signifikant. Det vill säga att det beräknade korrelationskoefficienten är osannolikt att vara ett resultat av ren slump. T.ex. alla dina 3 punkter kan lägga på samma linje, har detta en koefficient på +1 eller -1, men det skulle ändå vara resultatlösa.
- Då koefficienten är inte signifikant det i allmänhet ingen anledning att rapportera dess värde.
- Då korrelationen är viktig att du inte har bevisat att en variabel "orsakar" den andra. Du har bara visat att kunskapen om värdet av x kan bidra i viss mån förutsäga värdet på y eller tvärtom.
