Hur man kan beräkna flera tärningar sannolikheter

Räkning

1. 1
   Notera antalet tärningar, deras sidor, och den önskade summan.
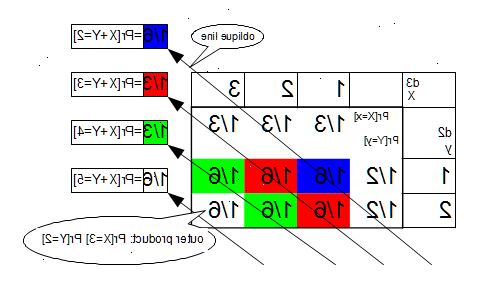
2. 2
   Räkna upp alla de sätt som summan kan nås. Detta kan vara långtråkig för ett stort antal tärningar, men är ganska enkel. Detta är ekvivalent med att hitta alla partitioner av k in exakt n delar med någon del större än r.. Ett exempel för n = 5, r = 6, och k = 12 visas som ett exempel. För att säkerställa att räkningen är både uttömmande och att ingen partition räknas två gånger, är skiljeväggarna presenteras i lexikografisk ordning och tärningarna i varje partition i icke-minskande ordning.
3. 3
   Inte alla partitioner som anges i föregående steg är lika sannolika. Det är därför de måste listas, inte bara räknas. I en mindre 3 die exempel täcker partition 123 6 möjligheter (123, 132, 213, 231, 312, 321) medan den partition 114 täcker endast 3 (114, 141, 411) och 222 endast omfattar själva. Använd multinomial formel för att beräkna antalet sätt att permutera siffror i varje partition. Denna information har lagts till i tabellen från föregående avsnitt.
4. 4
   Lägg det totala antalet sätt att få den önskade summan.
5. 5
   Dividera med det totala antalet resultat. Eftersom varje munstycke har r lika sannolika ansikten, är detta helt enkelt ^rn.

Rekursion

Denna metod ger sannolikheten för alla belopp för alla alla> antal tärningar. Det kan lätt implementeras på ett kalkylblad.

1. 1
   Notera sannolikheterna för resultaten av en tärning. Spela in dem i ett kalkylblad. Exemplet använder 6-sidiga tärningar. De tomma rader för negativa belopp behandlas som nollor och låta samma formel som skall användas i alla rader.
2. 2
   I kolumnen för 2 tärningar, använd formeln visas. Det är, lika med sannolikheten 2 tärningar som uppvisar någon summa k summan av följande händelser. För mycket höga eller låga värden på k, kan vissa eller alla eller dessa termer vara noll, men formeln är giltig för alla k.
   • Första tärningen visar k-1 och den andra visar 1.
   • Första tärningen visar k-2 och den andra visar två.
   • Första tärningen visar k-3 och den andra visar tre.
   • Första tärningen visar k-4 och den andra visar 4.
   • Första tärningen visar k-5 och det andra visar 5.
   • Första tärningen visar k-6 och den andra visar 6.
3. 3
   Likaså, för tre eller fler tärningar, gäller samma formel fortfarande, med hjälp av de nu kända sannolikheter för varje given summa på en die färre. Således kan formeln i steg två fyllas både nedåt och tvärs tills tabellen ingår så mycket data som krävs.
4. 4
   Kalkylbladet visas beräknade "antal sätt" inte "sannolikhet", men konvertering mellan dem är enkelt: sannolikhet = antal sätt / r ^ n där r är antalet sidor på varje dyna och n är antalet av tärningarna. Alternativt kan kalkylbladet modifieras för att beräkna sannolikhet direkt.

Genererande funktioner

1. 1
   Skriv polynomet, (1 / r) (x + x ² + x ^r). Detta är den genererande funktionen för en tärning. Koefficienten för x ^k sikt är sannolikheten att tärningen visar k..
2. 2
   Höj detta polynom till den n: ^te makten att få motsvarande genererande funktionen för summan som visas på n tärningar. Det är beräkna (1 / r ⁿ⁾ (x + x ² + x ^{r) n.} Om n är större än ca 2, kommer du förmodligen vill göra detta på en dator.
3. 3
   Beräkningsmässigt, är detta ekvivalent med den tidigare metoden, men ibland teoretiska resultat är lättare att härleda med en genererande funktion. Till exempel kastar två regelbundna 6-sidiga tärningar har exakt samma fördelning av belopp som en märkt form (1, 2, 2, 3, 3, 4) och en annan märkt (1, 3, 4, 5, 6, 8). Detta beror på att (x + x ² + x ² + x ³ + x ³ + x ⁴⁾ (x + x ³ + x ⁴ + x ⁵ + x ⁶ + x ⁸⁾ = (x + x ² + x ³ + x ⁴ + x ⁵ + x ⁶⁾ (x + x ² + x ³ + x ⁴ + x ⁵ + x ^6).

Kontinuerlig approximation

1. 1
   För ett stort antal tärningar kan exakt beräkning genom ovanstående metoder vara svårt. Centrala gränsvärdessatsen säger att en summan av ett antal identiska tärningar närmar sig en normal fördelning som antalet tärningar ökar.
2. 2
   Beräkna medelvärdet och standardavvikelsen variation baserat på antalet och typen av tärningar. Förutsatt n tärningar numrerade 1 till R, formlerna nedan gäller.
   • Den menar är (r +1) / 2.
   • Variansen är n (r ^ 2-1) / 12.
   • Standardavvikelsen är kvadratroten av variansen.
3. 3
   Använd normalfördelning med ovanstående medelvärde och standardavvikelse som en approximation av summan av tärningarna.