Hur man beräknar en kvadratrot för hand

Beräkna en kvadratrot för hand

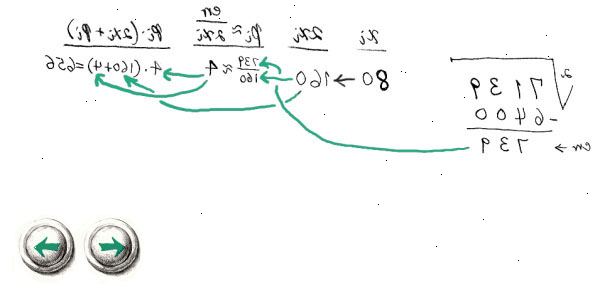
1. 1
   Skriv ner det nummer du vill beräkna kvadratroten av. Separera siffrorna i par, med början från decimaltecknet: 79,520,789,182.47897 blir "7 95 20 78 91 82 47 89 70.". Som ett exempel, försök att beräkna kvadratroten av 780,14. Rita två linjer som bilden visar och skriver "7 80. 14" till vänster. Uppe till höger, kommer du att ha kvadratroten av 780,14.
   
2. 2
   Titta på den vänstra paret och hitta det största heltalet n vars kvadrat är mindre än eller lika med den. Placera N i övre högra kvadranten, och beräkna kvadraten på n i den nedre högra kvadranten. I den här artikeln exempel är det paret 7. Och 2 × 2 ≤ 7 <3 × 3, alltså n = 2. Skriv 2 i övre högra kvadranten: det är den första siffran i kvadratroten. Skriv 2 × 2 = 4 i det nedre högra kvadranten, du kommer att behöva det numret i nästa steg.
   
3. 3
   Subtrahera numret du just räknat från den vänstra paret. För artikelns exempel subtrahera 4 från paret "7", vilket ger dig 3.
   
4. 4
   Släpp nästa par på vänster sida. Multiplicera antalet i övre högra kvadranten av två och skriva det i den nedre högra kvadranten, lägga "_ × _ =". I exemplet är nästa par "80": skriv "80" bredvid den 3. Sedan två gånger antalet längst upp till höger är 4: skriv "4_ × _ =" i det nedre högra kvadranten.
   
5. 5
   Hitta den största siffran att ersätta understryker så att resultatet av multiplikationen är lägre än eller lika med det aktuella numret till vänster. I exemplet, om du byter understreck med 8, 48 gånger 8 är 384, vilket är högre än 380. Därför 8 är för stor. Men 7 kommer att fungera. Skriv 7 på understreck och beräkna: 47 gånger 7 är lika med 329. Skriv 7 längst upp till höger: det är den andra siffran för kvadratroten av 780,14.
   
6. 6
   Subtrahera numret du just räknat från den aktuella numret till vänster. I exemplet, subtrahera 329 från 380, vilket ger 51.
   
7. 7
   Upprepa steg 4. Eftersom du nu möter decimalkommat i 780,14, skriva ett decimaltecken i kvadratroten, längst upp till höger. Släpp nästa par (14) till vänster. Två gånger numret längst upp till höger (27) är 54, så skriv "54_ × _ =" i det nedre högra kvadranten.
   
8. 8
   Upprepa steg 5 och 6. Hitta den största siffran att ersätta understreck och göra multiplikation. I exemplet, är 549 gånger 9 4941, vilket är lägre än eller lika med antalet till vänster (5114). Skriv 9 längst upp till höger, och subtrahera resultatet av en multiplikation av numret till vänster: 5114 minus 4941 är 173.
   
9. 9
   Om du vill fortsätta att räkna siffror, släppa ett par nollor till vänster, och upprepa steg 4, 5 och 6.
   

Förklara processen

1. 1
   För att förstå hur denna metod fungerar, titta på antalet du beräknar kvadratroten av eftersom området S i en kvadrat. Du försöker därför beräkna längden L av den sida av den kvadraten. Du vill hitta numret L så att L ² = S.
   
2. 2
   Antag att du ringer en den första siffran i L (kvadratroten vi försöker beräkna). B kommer att vara dess andra siffran, C sin tredje, och så vidare.
   
3. 3
   Antag att du ringer sa det första paret siffrorna s, sb det andra paret av siffror, osv.
   
4. 4
   Precis som i en division, där du bara är intresserad av nästa siffra i taget, här i kalkyl av kvadratroten, är du intresserad av de nästa två siffrorna i taget (som är nästa en siffra i tid för kvadratroten). Och också, precis som i en division, är läget för decimalkommat inte viktigt i processen: du kan alltid bara lägga den i slutet.
   
5. 5
   Titta på det första paret sa siffror för S (SA = 7 i exemplet) och du vill hitta sin kvadratroten. Den första siffran A av att kvadratroten är då den största heltal där torget inte överstiger Sa (dvs A så att A ² ≤ Sa <(A +1) ²). I exemplet, S1 = 7, och 2 ² ≤ 7 <3 ², så A = 2.
   
6. 6
   Observera att om du ville dela 88962 med 7, skulle det första steget vara liknande: du skulle titta på den första siffran 88962 (8) och du vill ha den största siffran som, när den multipliceras med 7, är lägre än eller lika till 8. Vilket betyder d så att 7 × d ≤ 8 <7 × (d +1). d skulle då vara lika med 1.
   
7. 7
   Beräkna nästa siffra B.
   
   • Betrakta (10A + B) ² = 100A ² + 2 × 10A × B + B ². (Kom ihåg att 10A + B är antalet med B i enheter positionen, och A i tiotals läge: med A = 1 och B = 2, 10A + B är helt enkelt antalet 12.)
     (10A + B) ^ är det område av hela kvadrat, 100a ² (10A + B) ²> området för den största kvadrat inuti, B ^ är den ytan av den minsta kvadrat, och 10a × b B ²> är arean för varje av de två rektanglarna.
8. 8
   I steg 3, subtraherar du ett ² från SA. Till grund för faktorn 100, släpper du ett par (Sb) siffror i S: du vill "Sa Sb" att vara den totala arealen av torget, och du subtraheras 100A ² (området stora torget) från den. Vad som återstår är talet N1 erhållits till vänster i steg 4 (380 i exemplet). Och den siffran är lika med 2 × 10A × B + B ² (area av de två rektanglarna plus området över det lilla torget).
   
9. 9
   Leta efter n1 = 2 × 10a × b + b ², även skrivet som n1 = (2 × 10a + B) × B. Du vet N1 (= 380) och A (= 2), och du letar efter B. I ekvation, är troligtvis B inte kommer att vara ett heltal, så du måste verkligen hitta det största heltal B så att (2 × 10A + B) × B ≤ N1. (Och B +1 skulle bli för stor, så du har:. N1 <(2 × 10A + (B +1)) × (B +1))
   
10. 10
    För att lösa detta, multiplicera A med 2, flytta den i läget för tiotals (vilket är ekvivalent med att multiplicera med 10), plats B i positionen av enheterna, och multiplicera den siffran med B. Det antalet är (2 × 10A + B) × B, och det är precis vad du gör när du skriver "N_ × _ =" (med N = 2 × A) i det nedre högra kvadranten i steg 4. Och i steg 5, hittar du det största heltal B som passar på understreck så att (2 × 10A + B) × B ≤ N1.
    
11. 11
    Subtrahera området (2 × 10a + B) × B från den totala arealen (till vänster, som i steg 6), vilket ger dig området s-(10a + b) ² inte stod ännu för (och som kommer att användas att beräkna de följande siffrorna på ett liknande sätt).
    
12. 12
    För att beräkna nästa siffra c, upprepa processen: släpp nästa par (Sc) från S att få N2 till vänster, och leta efter den största C så du har (2 × 10 × (10A + B) + C) × C ≤ N2 (detsamma som att skriva två gånger två-siffriga numret "AB" följt av "_ × _ =" och leta efter den största siffran som passar på understreck).