Wko

Hur bevisa Pythagoras sats

Den Pythagoras sats kan du räkna ut längden på den tredje sidan av en rätvinklig triangel när de andra två är kända. Och mer.
Den är uppkallad efter Pythagoras av Samos, som upptäckte och bevisade det. Han levde omkring 550 f.Kr. i Grekland. Det finns ingen anledning att tro satsen för att vara sant, kan du bevisa det, så du vet att det är.

Steg

Hur bevisa Pythagoras sats. Antag att vi har fyra kongruenta (grå) rätvinkliga trianglar.
Hur bevisa Pythagoras sats. Antag att vi har fyra kongruenta (grå) rätvinkliga trianglar.
  1. 1
    Antag att vi har fyra kongruenta (grå) rätvinkliga trianglar. Säger att de har ben av längd a, b och hypotenusan i längden c..
    Pythagoras sats säger att summan av kvadraterna av de två benen i en rätvinklig triangel är lika med kvadraten på hypotenusan. Så i princip behöver vi bevisa
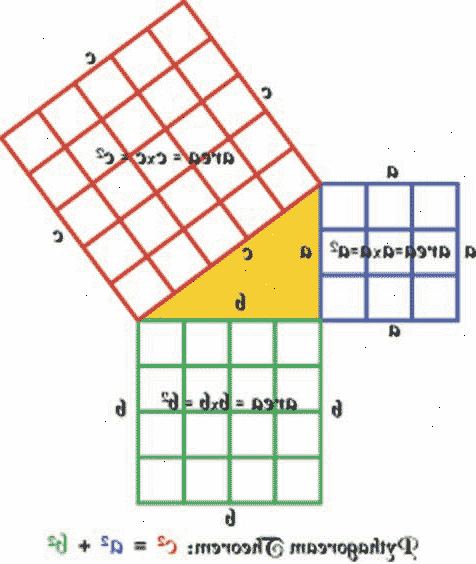
    a 2 + b 2 = c 2
  2. 2
    Ordna dem i en kvadrat med sidor (a + b) med (a + b), som den här.
    • Den gröna formen kvar av trianglarna ser lite ut som en kvadrat. Men är det verkligen en kvadrat?
    • Den har fyra lika sidor, är längden alltid c..
    • Du kan rotera (vrid) hela arrangemanget med 90 grader och det kommer att vara exakt samma. Du kan upprepa detta så många gånger du vill. Detta är endast möjligt om de fyra vinklarna i hörnen är lika.
    • Om du har fyra lika sidor och fyra lika stora vinklar du måste ha en kvadrat.
  3. 3
    Nu sätter samma fyra trianglar i samma ruta, men nu gör det annorlunda, som den här.
    • Den blå kvadrat har sidor av längd b, har den röda sidor av längden a.
  4. 4
    Jämför nu de två arrangemangen.
    • Den totala ytan av de två arrangemangen var densamma. I båda fallen använde vi en kvadrat med (a + b) med (a + b).
    • I båda arrangemangen vi täckte delvis ytan med exakt samma belopp, fyra grå trianglar som inte överlappar varandra.
    • Detta innebär att även området lämnas ut av trianglarna måste vara lika i båda arrangemangen.
    • Detta innebär att området för den blå och den röda fyrkant sammanlagt skall vara lika med arean av den gröna fyrkanten.
  5. 5
    Det blå området är en 2, det röda området b2 och grönområde c. 2.
  6. 6
    I korthet: a 2 + b 2 = c 2. Därför Pythagoras sats är bevisat!

Tips

  • Pythagoras sats gäller för rätvinkliga trianglar bara.
  • Du kan hitta andra matematiska bevis på. Inte alla high school grejer är där inne, men de jobbar på det.
  • Det finns oändligt många Pythagoras trillingar, där alla sidor av triangeln är heltal. Emellertid (3, 4, 5) och (5, 12, 13) är favorit bland matematik lärare.
  • Det är OK att tänka tvärtom. Om Pythagoras teorin gäller för en triangel, säger deras längder är 3, 4 och 5, måste det finnas en rät vinkel någonstans i denna triangel!
  • Det finns minst 367 olika sätt att satsen. Detta är ett av de enklaste.