Hur beräkna Laplacetransformen av en funktion

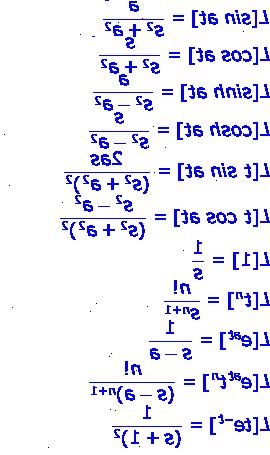
1. 1
   Veta om du försöker hitta den ensidiga (ensidiga) Laplace transform eller bilateralt (dubbelsidigt) Laplacetransformen av funktionen. Om den typ av Laplacetransformen inte anges, kan man anta att man bör beräkna den ensidiga version.
   • Ett ensidigt Laplacetransformen definieras som:
   • En bilateral Laplacetransformen definieras som:
2. 2
   Sätt din funktion, f (t), i definitionen av Laplacetransformen.

Terminologi

1. 1
   Betrakta "Laplacetransformer" - delvis det är ett system för att konvertera tidsberoende domän relationer till en uppsättning ekvationer uttryckta i Laplace-operatorn "s". Därefter lösningen av det ursprungliga problemet åstadkommes genom "komplex-algebra manipulationer" i "s" eller Laplace-domänen i stället för tidsdomänen:
   • "Tillämpa Laplace transformer är analogt med hjälp av logaritmer för att förenkla vissa matematiska operationer. Genom att ta logaritmer, siffror omvandlas till befogenheter 10 eller e (naturliga logaritmer). Som ett resultat av transformationer är matematiska multiplikationer och divisioner ersättas med tillägg och subtraktioner respektive. "
2. 2
   "Likaså gäller Laplacetransformer till analysen av system som kan beskrivas med linjära, ordinära tidsskillnaden övervinner något av den komplexitet som uppstått i tidsplanet lösning av sådana ekvationer.", Och, också:
   • Laplacetransformen innebär integrering från 0 till oändligheten av en tid variabel f (t) erhålls genom att multiplicera f (t) ^e-st.
   • f (t) är din tillämpad funktion som måste definieras för alla positiva värden på t.
   • s är en komplex algebra variabel definieras av: s = a + jo där j = sqrt (-1), så du kommer att vara delvis använda imaginära tal.
     • Symbolen i (j i elektroteknik) används för att representera √ -1. Därför, till exempel, √ (-4) = 2i. Antalet heter jag, eller 1i, eller xi kallas rent imaginära tal.
   • En användning av det komplexa planet är känt som s-planet. Det används för att visualisera rötterna till ekvationen som beskriver ett systems beteende (den karakteristiska ekvationen) grafiskt. Ekvationen uttrycks normalt som ett polynom i parametern "s" av Laplacetransformen, därav namnet "s" plan.
     • Komplexa planet med Argand Diagrammen visar z-planet, där z = x + iy och kan använda z-transformer samt Laplace. I matematik och signalbehandling, omvandlar Z-transform en diskret tidsdomänsignal, vilket är en följd av reella eller komplexa tal, till en komplex frekvens-domän representation. Det kan betraktas som en tidsdiskret ekvivalent av Laplacetransformen. Denna likhet är utforskas i teorin om tidsskalan kalkyl. Genom bilinjär transformation, är det komplexa s-planet (av Laplacetransformen) mappas till det komplexa z-planet (i z-transform).
       • Z = a + ib, = re ^ itheta, en = verklig del av z, b = imaginära delen av z, r = modul z, theta = argument av z, a & b är reella tal. Även denna kartläggning är (nödvändigtvis) olinjära, är det värdefullt att den visar hela jo axeln i s-planet på enhetscirkeln i z-planet, dvs, att jo axeln är i regionen av konvergens av Laplacetransformen.

Lösa transform

1. 1
   Utför integration med partiell integration. Beroende på din funktion, f (t) kan du behöva utföra partiell integration flera gånger för att fullt ut integrera integralen.
2. 2
   Sätt gränser i ditt resultat. Skriv ut ekvationen ersätter t med oändligheten sedan skriva ut det negativa i samma ekvation, denna gång ersätter t med 0. Förenkla detta ner så mycket du kan, komma ihåg följande värden:
3. 3
   Kontrollera ditt svar med hjälp av en tabell över Laplacetransformer.

Diskontinuerliga funktioner

En diskontinuerlig funktion kan skrivas som:

där c är en konstant och a och b kan vara antingen konstanter eller funktioner of t. Även om detta exempel har endast två delar, kan det finnas någon ändligt antal.

1. 1
   Skriv ut summan av Laplacetransformer av varje del av diskontinuerliga funktionen, med hjälp av de angivna gränserna, snarare än den vanliga 0 till ∞.
2. 2
   Beräkna Laplacetransformen som visas ovan. Kom ihåg att ersätta i de korrekta gränserna, snarare än 0 och ∞.
3. 3
   Förenkla resultatet som mycket som möjligt.

Använda egenskaper Laplacetransformer

1. 1
   Försök att härleda en Laplacetransformen av en funktion, om det liknar en eller flera andra funktioner, som du vet att transformera av. Till exempel:
   • Den Laplacetransformen av en linjär kombination av funktioner är samma linjär kombination av Laplacetransformationer.
   • Laplacetransformen av tf (t) är lika med-F "(s), där F (s) är Laplacetransformen av f (t) och F '(s) är dess derivat (Proof).
   • Den Laplacetransformen av f '(t) är lika med sF (s)-f (0).
   • Den Laplacetransformen av e ^ (at) f (t) är lika med F (sa).
   • Den Laplacetransformen av en faltning av två funktioner f och g är lika med produkten av deras Laplacetransformationer.
2. 2
   Använd de olika kända egenskaper Laplacetransformer att kunna härleda dem med hjälp av stegen ovan. Det är också bra att veta innebörden bakom varje fastighet.
3. 3
   Undersök detta förenklade generella uttalande, "Laplacetransformen av f (t) är lika med funktion F av er" och skriver: Laplace {f (t)} = F (s)
   • På samma sätt skulle den Laplacetransformen av en funktion g (t) skrivas: laplace {g (t)} = G (s)