Hur man använder Pythagoras sats

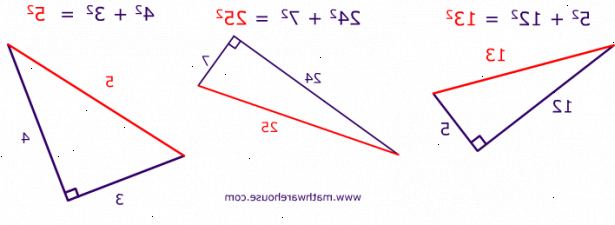
På rätvinkliga trianglar

1. 1
   Skriv ut Pythagoras sats: a ² + b ² = c ², och rita en bild av triangeln du löser.
2. 2
   Märk din ritning. Märk de kortare sidorna 'a' och 'b' (spelar ingen roll vilken sida som är A eller B), och etiketten hypotenusan (den längsta sidan, mitt emot den räta vinkeln) "c".
3. 3
   Bestäm vilken sida av triangeln du löser för: a, b eller c. Vanligtvis kommer du att få två av sidornas längder och använda formeln för att lösa för den tredje.
4. 4
   Skriv om ekvationen med de kända värdena.
   • Om du får de två sidornas längder (säg 3 och 4), skriv:
     3 ² + 4 ² = c ²
   • Om du får en sida och hypotenusan (3 & 5), skriv:
     3 ² + b ² = 5 ²
5. 5
   Beräkna rutorna.
   • Det första exemplet ovan bör skrivas om: 9 + 16 = c ².
   • Den andra: 9 + b ² = 25.
6. 6
   Kombinera liknande termer.
   • I detta fall alla villkor på den vänstra sidan av ekvationen är konstanta, så att vi kan lägga till dem för att få: 25 = c ².
   • I det andra exemplet måste du subtrahera 3 ² från båda sidor av ekvationen att isolera variabeln.
7. 7
   Ta kvadratroten.
   • Efter att ha tagit roten ur båda sidor av ekvationen, du är kvar med:
     c = 5.

Exempel: Med tanke på att hypotenusan är 10, och ett ben är 8, hitta längden av det andra benet.

A ^ + b ² = c ²

(8) ² + b ² = (10) ²

64 + b ² = 100

b ² = 100-64

b ² = 36

b = kvadratroten ur 36

b = 6

Exempel: En stege står lutad mot en byggnad. Basen i stegen är 5 meter från botten av väggen. Stegen når 20 meter upp väggen av byggnaden. Hur lång är stegen?

"5 meter från botten av muren": en = 5
"Når 20 meter upp på väggen" betyder b = 20
stegen längd är hypotenusa, så c är okänd

A ^ + b ² = c ²

(5) ² + (20) ² = c ²

25 + 400 = c ²

425 = c ²

c = kvadratroten av 425

c = 20,6 (avrundat till närmaste tiondel)

Så den ungefärliga längden på stegen är 20.6 meter.

Som en del av avståndet formel

Avståndet formeln används i geometri för att hitta det rätlinjiga avståndet mellan två punkter.

1. 1
   Bestäm vad pekar använda. Normalt poäng ges som ordnade parvis.
2. 2
   Plotta punkter på en graf. (X, y), där x är den horisontella axeln, och y är den vertikala.
3. 3
   Hitta längden på sidorna av triangeln. Du kan göra detta genom att räkna skillnaden i diagrammet, eller med hjälp av (x ₁ - x ₂₎ för x, och (y ₁ - y ₂₎ för y.
4. 4
   Använd Pythagoras sats. Avståndet mellan punkterna är hypotenusan av triangeln.

Exempel:
3 - 6 = -3 (x)
(-3) ² + (4) ² = c ²
c = sqrt (25)

På icke-rätvinkliga trianglar med hjälp av trigonometri

Detta avsnitt använder exemplet med de två städerna från ovan, i det här fallet måste du lösa för avståndet från staden A till City C.
För detta exempel antar sidor 'a' och 'b' är kända (se bilden nedan).

1. 1
   Rita en bild av din triangel.
2. 2
   Rita höjden. En höjd är en linje som är vinkelrät mot hypotenusan som passerar genom den motsatta vertex. I detta fall är höjden är 'c.'
3. 3
   Mät vinkeln mellan linjen som förbinder staden A till B och höjden linjen.
   
   • Typiskt vinkeln kommer att ges på denna typ av problem. Om inte, mäta vinkeln med en gradskiva.
4. 4
   Använd trigonometriska funktionen för att hitta längden på höjden:
   Om längden "a" är känd, och sedan: Cos (A) = c / a och c = Acos (A)
5. 5
   Använd Pythagoras sats för att hitta längden på linjen från staden A till höjden:
   x1 = sqrt (a ² - c ²⁾
6. 6
   Använd Pythagoras sats för att hitta avståndet mellan höjd linjen och stad C: x2 = sqrt (b ² - c ²⁾
7. 7
   Ta summan av x1 och x2.
8. 8
   Exempel: Du bor i staden A och har en vän som bor i staden C, och du vill veta hur långt din vän bor från dig. Du vet dess om en 50 mil bilresa till City B, sedan ytterligare 100 miles därifrån till City C. Hur lång är en rak linje från City A till stad C? (Avrunda alla beräkningar till närmaste tiondel)
   
   • Rita höjden linjen och mäta vinkeln.
     
   • Använd cosinusfunktionen att hitta längden på höjden:
     längd = 50 x cos (30) = 50 x 0,866 vilka rundor till 43,3 miles
   • Använd Pythagoras sats för att hitta längden på X1:
     x1 = sqrt (50 ^{2-43,3 2)} = sqrt (625,11) = 25.0 miles
   • Använd Pythagoras sats för att hitta längden på avståndet x2:
     x2 = sqrt (100 ^{2-43,3 2)} = sqrt (8125,1) = 90,1 miles
   • Lägg de två avstånden tillsammans för att hitta den totala sträckan:
     

I vektoraddition

Pythagoras sats används vid lösandet för resulterande vektorer. Detta görs genom att bryta vektorerna in i "x" och "y" komponenterna (och "z" i 3d), och tillsats av lika komponenter. De resulterande komponenterna (sidorna av rätvinklig triangel) kan användas för att lösa ut den resulterande (hypotenusan).

1. 1
   Bryt dina vektorer i x-och y-komponenter. Vektorer har riktning och storlek, riktningen är vinkeln skapade moturs från den positiva x-axeln, och storleken är längden av vektorn. Att bryta vektorn i komponenter, kommer du att använda trigonometri. Till exempel kan en vektor med magnituden "M" och vinkel 30 ":
   • x = M * cos (30)
   • y = M * sin (30)
2. 2
   Lägg lika komponenter. Nu när dina vektorer är uppdelade i x-och y-komponenterna, ta summan av x-komponenterna och summan av y-komponenterna. Dessa är de sidor av triangeln.
3. 3
   Använd Pythagoras sats. I detta fall (summan av x) ² + (summan av y) ² = c ², där "C" är den resulterande storleken.

Exempel:
[10cos (30) + 15cos (45)] = 19.27 (avrundat till närmaste hundradel) (x)
(19.27) ² + (15.61) ² = c ²
c = sqrt (615,005)