Visualisera två punkter, A och B, som förbinds med en rät linje segment. Nu föreställa sig att rita en andra linje rakt genom mitten av den första, vid exakt 90 grader mot den första. Denna andra raden är en mittpunktsnormalen.
Geometriskt sett är en mittpunktsnormalen en grupp av punkter (tekniskt, ett "locus") som är lika långt från både A och B. Formen gruppen alltid bildar en linje. Varje punkt på mittpunktsnormalen är så långt från punkt A från punkt B. I artikeln beskrivs hur du hittar ekvationen för mittpunktsnormalen, förutsatt att du har koordinaterna för punkterna A och B.
Steg
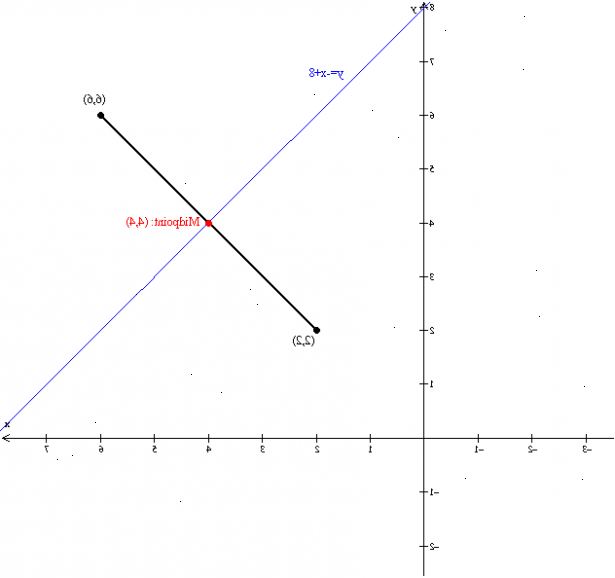
- 1Hitta lutningen mellan två punkter. För information om hur man gör det, vänligen se artikeln Hur förstå lutning (i algebra).
- 2Ta den lutning och hitta sin negativa ömsesidig. Med andra ord, vänd på fraktionen över, och ändra dess tecken.
- Exempel: om du börjar med 4/9, är den negativa reciproka -9/4.
- Exempel: om du börjar med 5, du förvandla den till en bråkdel genom att sätta en 1 under den, så här: 5/1. Då är det negativa reciproka -1/5.
- Exempel: om du börjar med -7/3, är den negativa reciproka 3/7.
- Kom ihåg, om du börjar med en negativ del, kommer den negativa reciproka hamna positivt!
- 3Hitta mittpunkten av de två punkter. Mittpunkten ligger på linjen från A till B, halvvägs mellan A och B.
- lägga till x-koordinaten för A med x-koordinaten för B, sedan dividera med två. Detta är den nya x-koordinaten för mittpunkten.
- Lägg y-koordinaten för A med y-koordinaten för B, sedan dividera med två. Det här är y-koordinaten för mittpunkten.
- 4Med hjälp av denna mittpunkt, och den negativa reciproka från steg 2, beräkna ekvationen för linjen. För mer information om hur du gör detta, se artikeln Så hittar ekvationen för en linje.
