Rätvinklig trig är användbar när du arbetar med trianglar och är en fundamental del av trigonometri i allmänhet. Vanligtvis är rätt trig en students första möte med trig, och det kan vara lite förvirrande i början. Dessa steg kommer att klargöra trigonometriska nyckeltal och hur de används.
Steg
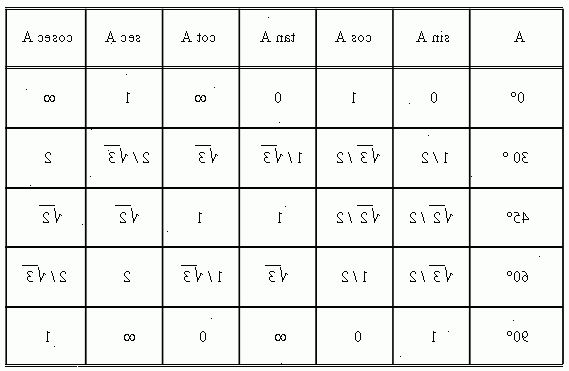
- 1Vet de 6 trigonometriska förhållandena. Du måste memorera följande:
- sinus
- förkortat som synden
- motsatta / hypotenusa
- cosinus
- förkortat cos
- angränsande / hypotenusa
- tangent
- förkortat som solbränna
- motsatt / intilliggande
- cosekant
- förkortat csc
- hypotenusan / motsatt
- sekant
- förkortat sek
- hypotenusan / intilliggande
- cotangens
- förkortat barnsäng
- intilliggande / motsatt
- sinus
- 2Upptäck mönster. Oroa dig inte om du är förvirrad över vad allt betyder just nu och inte galen om att memorera allt. Det är inte så svårt om du vet de mönster:
- Förkortningarna används alltid när du skriver ut trigonometriska funktioner. Du kommer aldrig att skriva ut cotangens eller sekant. När du ser förkortningen, bör du höra namnet. Likaså när du hör namnet, bör du höra förkortningen. Notera att i samtliga fall utom csc (cosekant), är förkortningen de tre första bokstäverna i namnet. CSC är ett undantag eftersom de tre första bokstäverna är "cos" som redan används. Så i stället är det de första tre konsonanter.
- Du kan komma ihåg de första tre nyckeltal med följande: Sohcahtoa. Tänk bara på det som ett namn att komma ihåg. Gör honom en Aztec Chieftain om det hjälper dig att komma ihåg det, se bara till att du kommer ihåg hur man stavar det. Det är i princip den första bokstaven "s i o synd> pposite h ypotenuse, c hypotenusan> os en djacent h angränsande> ypotenuse, t en o tan> pposite en djacent" Observera att om du sätter ordet över mellan två ord som är inte trig förhållanden (dvs. intill och hypotenusan, inte cos och intill), efter namnet på varje trig funktion är dess ratio.
- De tre sista är bara reciprocals av de tre första (inte inverser). Kom ihåg att vad som helst utan ett prefix "co" har en ömsesidig med prefixet, och allt med ett prefix "co" har en omvänd funktion utan prefix. Därför, CSC, sek, och spjälsäng trigonometriska förhållanden är reciproka av sin, cos och tan förhållanden resp. Till exempel är spjälsäng s förhållande intill över motsatsen.
- Förkortningarna används alltid när du skriver ut trigonometriska funktioner. Du kommer aldrig att skriva ut cotangens eller sekant. När du ser förkortningen, bör du höra namnet. Likaså när du hör namnet, bör du höra förkortningen. Notera att i samtliga fall utom csc (cosekant), är förkortningen de tre första bokstäverna i namnet. CSC är ett undantag eftersom de tre första bokstäverna är "cos" som redan används. Så i stället är det de första tre konsonanter.
- 3Vet de delar av triangeln. Du vet förmodligen vad hypotenusan är på denna punkt, men du kan vara lite förvirrad över de motsatta och angränsande sidor. Titta på följande diagram: Dessa sidor är korrekt när du använder vinkeln C. Om du ville använda vinkeln A, skulle orden motsatta och angränsande vändas i diagrammet.
- 4Förstå vad de trigonometriska förhållandena är och när de används. När rätvinklig trig först upptäcktes, insåg man att när du har två rätvinkliga trianglar som liknar (dvs den vinkel som uppmäts är samma), om du delar en sida med en annan och göra samma sak med de motsvarande sidorna av den andra triangeln, skulle du få samma värden. De trigonometriska funktionerna därefter utvecklas så att du kan hitta förhållandet för en given vinkel. Sidan Namnen gavs också att göra det lättare att avgöra vilka vinklar som ska användas. Du kan använda trigonometriska nyckeltal för att avgöra en sida åtgärd eftersom en av sidorna och en vinkel, eller så kan du använda dem för att bestämma en vinkel åtgärd ges två sido längder.
- 5Räkna ut vad du vill lösa. Markera det okända värdet med ett "x". Detta kommer att hjälpa dig att ställa in ekvationen senare. Kontrollera också att du har tillräckligt med information för att lösa triangeln. Du behöver antingen en vinkel och en sida eller alla tre sidor.
- 6Ställ upp förhållandet. Märk den motsatta sidan, intill sidan och hypotenusan med avseende på den markerade vinkeln (det spelar ingen roll om märket är ett nummer eller en "x" från föregående steg). Sedan skriva ner vilka sidor du antingen vet eller vill hitta. Utan tanke på CSC, sekund, eller barnsäng, avgöra vilka förhållandet involverar båda sidorna du skrev ner. Du bör inte använda de ömsesidiga förhållandena eftersom det finns oftast ingen miniräknare knapp för dem. Även om du kan, kommer det nästan aldrig vara en situation där du kommer att behöva använda dem för att lösa en rätvinklig triangel. När du vet vilken kvot att använda, skriva ner, följt av värdet eller variabel av triangeln. Skriv sedan ett likhetstecken följt av sidorna förhållandet encompasses (fortfarande i termer av motsatt, intill, och hypotenusan). Skriv om ekvationen, fyller i sidan längder / variabel i förhållandet.
- 7Lös ekvationen. Om variabeln är utanför trig-funktionen (det betyder att du skulle lösa för en sida), sedan bara lösa det exakta värdet av x anslut sedan uttrycket i din räknare för en närmevärde av sidans längd. Om din variabel är inne argumentet av trig-funktionen (det betyder att du skulle lösa för en vinkel), så ska du förenkla uttrycket till höger sedan kontakten inversen av att trig funktion följt av uttrycket. Till exempel, om din ekvation var sin (x) = 2/4, då du skulle förenkla den högra sidan för att få 1/2, och sedan stansa in din miniräknare "synd -1" (det är alla en knapp, oftast det andra alternativet för trig funktion du vill) följt av 1/2. Se till att när du gör beräkningar, du är i rätt läge. Om du vill ha grader, lägg din miniräknare i examen läge, om du vill radianer, sätta din miniräknare i radian-läge, om du inte vet vad grader eller radianer, sätta din miniräknare i examen läget. Värdet på x är värdet av den sida eller vinkel du försökte hitta.
Tips
- synd -1 är inte samma sak som CSC, är cos -1 inte samma sak som sekund, och tan -1 är inte samma sak som barnsäng. Den första är den inversa trigonometriska funktionen, vilket innebär att om du sätter in värdet på ett förhållande, kommer det att ge dig motsvarande vinkel, den andra är omvänd funktion vilket förhållandet är omvänd.
- Värdena för sin och cos är alltid mellan -1 och 1, men tangent kan vara valfritt antal. Om du får ett felmeddelande om inversa trigonometriska funktionen, är ditt värde förmodligen för stort eller för litet. Kontrollera din ratio och försök igen. Ett vanligt fel är att vända sidorna i förhållandet, som att använda hypotenusan / motsatsen för synd.
