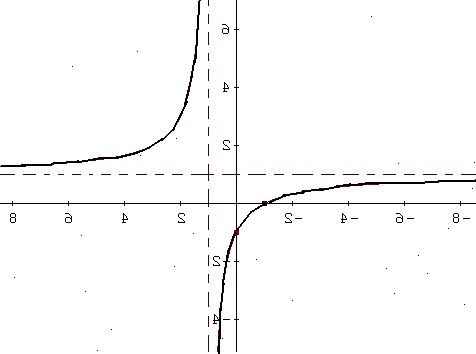
En rationell funktion är en ekvation som tar formen y = N (x) / D (x) där N och D är polynom. Försök att skissa en korrekt kurva av en hand kan vara en heltäckande översyn av många av de viktigaste höga ämnen skolamatte från grundläggande algebra till differentialkalkyl. Betrakta följande exempel: y = (2 x 2 - 6 x + 5) / (4 x + 2).
Steg
- 1Hitta den skärningspunkt med y. Ställ bara in x = 0. Allt utom de konstanta termerna försvinner, lämnar y = 5/2. Att uttrycka detta som en koordinat par (0, 5/2) är en punkt på grafen. Graf den punkten.
- 2Hitta den horisontella asymptot. nämnaren i täljaren att avgöra beteendet hos y för stora absoloute värden på x. I detta exempel visar division att y = (1/2) x - (7/4) + 17 / (8 x + 4). För stora positiva eller negativa värden på x, 17 / (8 x + 4) närmar sig noll, och grafen approximerar linjen y = (1/2) x - (7/4). Med hjälp av en streckad eller lätt dragen linje, kurva denna linje.
- Om av täljare är mindre än den grad av nämnaren, det finns ingen uppdelning att göra, och det asymptot är y = 0.
- Om deg (N) = deg (D), är asymptoten en horisontell linje i förhållandet de ledande koefficienter.
- Om deg (N) = deg (D) + 1, är asymptoten en linje vars lutning är förhållandet mellan de ledande koefficienter.
- Om deg (N)> deg (D) + 1, då för stora värden på | x |, y snabbt går till positiv eller negativ oändlighet som en kvadratisk, kubisk, eller högre grad polynom. I detta fall är det förmodligen inte värt att exakt graf kvoten av divisionen.
- 3Hitta nollorna. En rationell funktion har en nolla när det är täljaren är noll, så satt N (x) = 0. I exemplet, 2 x 2 - 6 x + 5 = 0. Diskriminantanalys av denna kvadratiska är b 2 - 4 för ac = 02 till 04 Juni * 2 * 5 = 36 - 40 = -4. Eftersom diskriminantanalys är negativt, N (x), och följaktligen f (x), har inga reella rötter. Grafen skär aldrig x-axeln. Om några nollor hittades, tillsätt dessa punkter i grafen.
- 4Hitta de vertikala asymptoter. En vertikal asymptot uppstår när nämnaren är noll. Inställning 4 x + 2 = 0 ger den vertikala linjen x = -1 / 2. Diagram varje vertikal asymptot med en ljus eller streckad linje. Om något värde för x gör både N (x) = 0 och D (x) = 0, kan det eller kan inte vara en vertikal asymptot där. Detta är ovanligt, men se tips för hur man handskas med det om det inträffar.
- 5Titta på resten av divisionen i steget 2. När är det positivt, negativt eller noll? I exemplet, är täljaren av återstoden 17 som alltid är positiv. Nämnaren, 4 x + 2, är positiv till höger om den vertikala asymptot och negativa åt vänster. Detta innebär att grafen närmar den linjära asymptot från ovanstående för stora positiva värden på x och underifrån för stora negativa värden på x. Sedan 17 / (8 x + 4) aldrig kan vara noll, denna graf aldrig skär linjen y = (1/2) x - (7/4). Lägg inte något till grafen just nu, men observera dessa slutsatser till senare.
- 6Hitta den lokala extrempunkter. En lokal extremum kan inträffa närhelst N '(x) D (x) - N (x) D' (x) = 0. I exemplet, N '(x) = 4 x - 6 och D' (x) = 4. N '(x) D (x) - N (x) D' (x) = (4 x - 6) (4 x + 2) - (2 x 2 - 6 x + 5) * 4 = 0. Expanderande, kombinera termer, och dividera med 4 blad x 2 + x - 4 = 0. Den kvadratiska formel visar rötter nära x = 3/2 och x = -5 / 2. (Dessa skiljer sig från cirka 0,06 från exakta värden, men vår grafen kommer inte att vara tillräckligt exakt för att oroa sig detaljnivå. Välja en anständig rationell approximation gör nästa steg lättare.)
- 7Hitta de y-värden för varje lokal extremum. Anslut de x-värden från föregående steg tillbaka till den ursprungliga rationell funktion för att hitta motsvarande y-värden. I exemplet, f (3/2) = 1/16 och f (-5 / 2) = -65/16. Lägg dessa punkter, (3/2, 1/16) och (-5 ° / 2, -65/16), till grafen. Eftersom vi approximerade i föregående steg, dessa are't den exakta minima och maxima, men är förmodligen nära. (Vi vet (3/2, 1/16) ligger mycket nära den lokala minimum. Från steg 3, vi vet att y är alltid positiv när x> -1 / 2 och vi hittade ett värde så liten som 1/16, så åtminstone i detta fall är felet troligen mindre än tjockleken av linjen.)
- 8Ansluta prickar och smidigt utöka grafen från de kända punkterna till asymptoter tar hand att närma sig dem från rätt håll. Se till att inte korsa x-axeln utom på de punkter som redan finns i steg 3. Korsa inte den horisontella eller linjär asymptot utom på de punkter som redan finns i steg 5. Ändra inte från uppåtlutande till nedåtgående utom vid extrema hittades i föregående steg.
Tips
- Om du följer stegen i ordning är det vanligtvis inte nödvändigt att använda andraderivatan tester eller liknande potentiellt komplicerade metoder för att avgöra om de kritiska värdena är lokala maxima, lokala minima, eller ingetdera. Försök att använda information från tidigare steg och lite logik först.
- Vissa av dessa åtgärder kan innebära att lösa en hög grad polynom. Om du inte kan hitta exakta lösningar genom faktorisering, formler eller andra medel, sedan uppskatta de lösningar med hjälp av numeriska metoder såsom Newtons metod.
- Om du försöker göra detta med bara Precalculus metoder, kan du byta ut stegen om att hitta lokala extrempunkter genom att beräkna flera ytterligare (x, y) beställde parvis mellan varje par av asymptoter. Alternativt, om du inte bryr dig varför det fungerar, det finns ingen anledning till varför en Precalculus elev inte kan ta derivatan av ett polynom och lösa N '(x) D (x) - N (x) D' (x) = 0.
- I sällsynta fall kan den täljare och nämnare har en gemensam icke-konstant faktor. Om du följer stegen, skulle detta visa sig som en nolla och en vertikal asymptot på samma ställe. Det är omöjligt och vad som faktiskt händer är en av följande:
- Den noll i N (x) har högre multiplicitet än noll i D (x). Grafen av f (x) närmar sig noll vid denna punkt, men är odefinierad där. Ange detta med en öppen cirkel runt punkten.
- Den noll i N (x) och noll i D (x) har samma mångfald. Grafen närma vissa icke-noll poäng för detta värde på x, men är odefinierad där. Återigen visar detta med en öppen cirkel.
- Den noll i N (x) har lägre multiplicitet än noll i D (x). Det är en vertikal asymptot här.
