Enhetscirkeln är det bästa verktyget för att ha när det handlar om trigonometri, om du kan verkligen förstå vad enhetscirkeln är och vad den gör, kommer du att hitta trig mycket enklare.
Steg
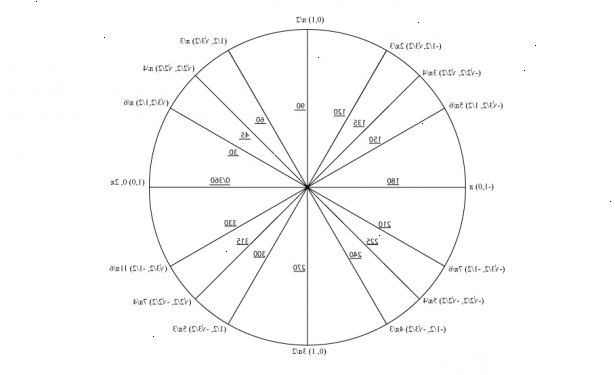
- 1Vet vad enhetscirkeln är. Enheten cirkel är en cirkel, som är centrerad vid origo, med en radie på 1. Minns från conics att ekvationen är x 2 + y 2 = 1. Denna cirkel kan användas för att hitta vissa "speciella" trigonometriska nyckeltal samt stöd i grafer. Det finns också ett reellt tal linje lindad runt cirkeln som fungerar som ingångsvärde vid utvärdering trigonometriska funktioner.
- 2Vet de 6 trigonometriska förhållandena. Vet att
- sinö = motsatta / hypotenusa
- cosö = angränsande / hypotenusa
- tanö = motsatta / intilliggande
- cscθ = 1/sin
- secθ = 1/cos
- cotθ = 1/tan.
- 3Förstå vad en radian är. En radian är ett annat sätt att mäta en vinkel. En radian är den vinkel som behövs så det inneslutna båglängd är lika med radien längd. Observera att det inte spelar någon roll hur stor eller orientering av cirkeln. Du måste också veta hur många radianer i en full cirkel (360 grader). Kom ihåg att omkretsen av en cirkel ges av 2πr så det finns 2π radie åtgärder runt omkretsen. Eftersom en radian per definition är den vinkel där radie längd är lika med båglängden, finns 2π radianer i en hel cirkel.
- 4Kunna konvertera mellan radianer och grader. Det finns 2π radianer i en full cirkel, eller 360 grader. Så:
- 2πradian = 360 graders
- radian = (360/2π) examen
- radian = (180 / π) examen
- och
- grad = 2πradian
- grad = (2π/360) radianer
- grad = (π/180)
- 5Vet de "särskilda" vinklar. De speciella vinklar i radianer är π / 6, π / 3, π / 4, π / 2, π, och multiplar av alla (t.ex. 5π / 6)
- 6Känna och memorera trigonometriska identiteter som ger 6 trigonometriska funktioner för alla vinklar. För att härleda dessa, måste du titta på enhetscirkeln. Minns att det finns ett reellt tal linje lindad runt enhetscirkeln. Den punkt på antalet linje avser antalet radianer i den bildade vinkeln. Till exempel Punkten π / 2 på det verkliga antalet linjen motsvarar den punkt på cirkeln vars radie bildar en vinkel på π / 2 med den positiva horisontella radie. Konsten att hitta de trigonometriska värdena valfri vinkel, är därför att hitta koordinaterna för punkten. Hypotenusan är alltid 1, eftersom det är radien på den cirkel, och eftersom valfritt antal delat med en i sig, och den motsatta sidan är lika med y-värde, följer det att sinusvärdet är y-koordinaten för punkten. Cosinus värde följer en liknande logik. Cos är lika med den närliggande sidan dividerat med hypotenusan, och igen, såsom hypotenusan är alltid 1, och den intilliggande sidan är lika med x-koordinat, följer det att cosinus värdet är x-koordinaten för punkten. Tangenten är något svårare. Tangenten för en vinkel i en rätvinklig triangel är lika med den motsatta sidan dividerad med den intilliggande sida. Problemet är att det inte finns något konstant i nämnaren som i de tidigare exemplen, så du måste vara lite mer kreativ. Kom ihåg att den motsatta sidan är lika med y-koordinat och den intilliggande sidan lika med x-koordinat, så genom att ersätta, bör du finna att tangenten motsvarar y / x. Med denna kan du hitta de inversa trigonometriska funktionerna genom att ta det reciproka värdet av dessa formler. För att sammanfatta, här är identiteterna.
- sinö = y
- cosö = x
- tanö = y / x
- CSC = 1 / y
- sek = 1 / x
- spjälsäng = x / y
- 7Hitta och memorera 6 trigonometriska funktioner för vinklar på axlarna. För vinklar som är multiplar av π / 2 till exempel 0, π / 2, π, 3π / 2, 2π etc. Att hitta trigonometriska funktioner är lika enkelt som föreställande vinkeln på axlarna. Om terminalen sidan är längs x-axeln, kommer synden att vara 0 och cos blir antingen 1 eller -1 beroende på vilken riktning ray poäng. Likaså, om terminalen sidan är längs y-axeln, kommer synden att vara antingen 1 eller -1 och cos blir 0.
- 8Hitta och memorera 6 trigonometriska funktioner speciella vinkeln π / 6. Börja med att rita av vinkeln π / 6 på enhetscirkeln. Du vet hur man hittar sidornas längder för speciella rätvinkliga trianglar (30-60-90 och 45-45-90) givna ena sidan, och som π / 6 = 30 grader, är denna triangel är en av dessa speciella fall. Så om ni minns, är det korta benet 1/2 hypotenusan, så y-koordinaten är 1/2, och det långa benet är √ 3 gånger det kortare benet, eller (√ 3) / 2, så att x-koordinat är (√ 3) / 2. Koordinaterna för den punkten är ((√ 3) / 2,1 / 2) Nu använder identiteter i föregående steg för att finna att:
- sinπ / 6 = 1/2
- cosπ / 6 = (√ 3) / 2
- tanπ / 6 = 1 / (√ 3)
- cscπ / 6 = 2
- secπ / 6 = 2 / (√ 3)
- cotπ / 6 = √ 3
- 9Hitta och memorera 6 trigonometriska funktioner i det särskilda vinkeln π / 3) vinkeln π / 3 har en punkt på omkretsen där x-koordinaten är lika med y-koordinaten i π / 6 vinkel, och y-koordinat är samma som x-koordinat. Så, är den punkt (1/2, √ 3/2). Därför följer att:
- sinπ / 3 = (√ 3) / 2
- cosπ / 3 = 1/2
- tanπ / 3 = √ 3
- cscπ / 3 = 2 / (√ 3)
- secπ / 3 = 2
- cotπ / 3 = 1 / (√ 3)
- 10Hitta och memorera 6 trigonometriska funktioner speciella vinkeln π / 4. Förhållandena för en 45-45-90 triangel är en hypotenusa √ 2 och ben 1, så på enhetscirkeln, måtten är följande: och de trigonometriska funktionerna är:
- sinπ / 4 = 1 / (√ 2)
- cosπ / 4 = 1 / (√ 2)
- tanπ / 4 = 1
- cscπ / 4 = √ 2
- secπ / 4 = √ 2
- cotπ / 4 = 1
- 11Vet vilka hänvisning vinkel att använda. Vid denna punkt du redan har hittat de trigonometriska värdena för de tre särskilda referens vinklar, men alla dessa är i kvadrant I. Om du behöver hitta en funktion av en större eller mindre speciell vinkel, först räkna ut vilken referens vinkel är i samma "familj" av vinklar. Till exempel består den π / 3 familj av 2π / 3, 4π / 3, och 5π / 3. En bra allmän regel för att hitta referensvinkeln är att minska fraktionen så mycket som möjligt sedan titta på botten nummer. # * Om det är en 3, är den i π / 3 familj
- Om det är en 6, är det i π / 6 familj
- Om det är en 2, är det i π / 2 familj
- Om den står ensam, liksom π eller 0, är det i π familjen
- Om det är en 4, är den i π / 4 familj
- 12Vet huruvida värdet är positivt eller negativt. Alla vinklar i samma familj har samma trigonometriska värden som referens vinkel, men 2 kommer att vara positiv och två kommer att vara negativ.
- Om vinkeln är i kvadrant I, alla trigonometriska värden är positiva
- Om vinkeln är i kvadrant II, alla trigonometriska värden är negativa utom synden och CSC.
- Om vinkeln är i kvadrant III, alla trigonometriska värden är negativt förutom tan och spjälsäng.
- Om vinkeln är i kvadrant IV, alla trigonometriska värden är negativa utom för cos och sek.
