Velocity är vanligtvis hittas genom att dividera förskjutning genom tagit tid, men resultatet representerar den genomsnittliga hastigheten under hela resan eller tidsperiod. Läs den här artikeln att ta reda på hur man beräknar hastigheten över en oändligt liten tid.
Steg
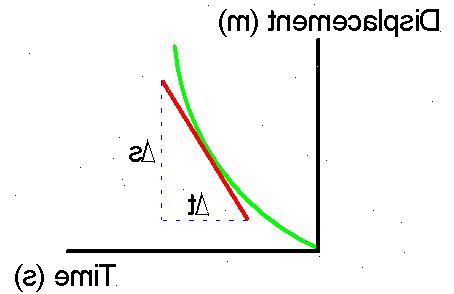
- 1Börja med en väg som resas mindre, förskjutning, att det tagit tid.
- 2Vi kommer att ringa förskjutning = s
- 3Tid = t
- 4Velocity = v
- 5Gradient = m
- 6^ Tecknet är att "makt"
- 7(Till exempel) Slagvolym (s) = 2t ^ 2-4T 7.
- 8Velocity (v) vid tiden (t) är lika med lutningen (förändringshastigheten) för den funktion som relaterar förskjutning (s) till tiden (t).
- 9Den derivatan av en funktion är lika med gradienten av funktionen på något ställe. För att hitta derivatan du skilja funktionen så här:
- 10Allmän regel för att hitta derivatan: Om y = a * x ^ n
- 11Derivat = a * n * x ^ n-1
- 12Denna regel tillämpas på varje termin av polynom, kommer den konstanta termen (den term som inte multiplicerar med x variabeln) försvinner eftersom det kommer att multipliceras med 0.
- 13Räkneexempel: y = 3x ^ 2 + 4x + 7
- 14Derivata = (3 * 2) * x ^ (2-1) + (4 * 1) * x ^ (1-1) + (7 * 0) * x ^ (0-1)
- 15= 6x ^ 1 + 4x ^ 0 + 0x ^ -1
- 16= 6x + 4
- 17Därför gradienten av funktionen kommer alltid att vara lika med 6x + 4.
- 18För att hitta momentanhastigheten du kommer att använda ovanstående metod för att differentiera ekvationen om (s) till (t), kommer detta att ge dig den formel som relaterar hastigheten till tid.
- 19För att hitta acceleration skulle du använda den metod som visas för att differentiera ekvation gäller hastigheten på tiden, därför att hitta ekvationen för acceleration du först måste hitta ekvationen för hastigheten.
- 20Vad som följer är en förklaring av där processen med differentiering kom ifrån.
- 21Tänk att y-axeln i diagrammet är förskjutningen skala och x-axeln är tidsskalan, så bilden kan gå under x-axeln, men det kommer aldrig att gå bakom y-axeln, skulle detta innebära att gå tillbaka i tid.
- 22Nu i ditt sinne du har en graf. Gradienten av en graf är förändringshastigheten av y dividerad med ändringshastigheten för x. Så om Y är förskjutning och X är tid, är gradienten ändringstakten av förskjutning dividerad med graden av förändring av tid, är detta uppenbarligen hastighet!
- 23Så nu vad vi behöver är att hitta lutningen på grafen i någon punkt. Jag kommer att förklara processen från första principer, kan du hoppa till steg () om du vill.
- 24För att göra detta använder vi ett trick som kallas att ta en gräns, med en gräns innebär att man tar två punkter P och Q på böjda grafen och hitta lutningen på linjen som förbinder dem som avståndet mellan dem blir mindre.
- 25Ta P vara den punkt på grafen där X (eller egendomen på X-axeln) är lika med 1, är värdet inte av konsekvens så att du kan välja ett lämpligt värde.
- 26Ta Q för att vara den punkt där X är lika, till exempel, 3.
- 27Nu arbetar du ut gradienten mellan P och Q, med skillnaden mellan X värdet av P och X-värdet för Q kallas, till exempel, H.
- 28Nu kan du minska H med en liten bit, IE: föra Q närmare p på X-axeln och beräkna gradienten mellan P och Q. Du kommer att börja se efter några omräkningar att lutningen tenderar mot en gräns, är det långsamt komma närmare ett värde men kommer inte riktigt få till det så länge H> 0. Värdet att lutningen tenderar mot som H tenderar mot 0 är gränsen, tas detta som lika med lutningen av tangenten till kurvan som erkänns som parallellt med kurvan för en oändligt liten tid. Den gradient för tangenten är därför kurvans lutning vid punkten P.
- 29Ekvationen för lutningen för tangenten kallas härledda ekvationen, är det så du hittar det algebraiskt.
- 30Derivatan eller härledda funktionen skrivs som dy över dx.
- 31Om kraften i X i den första termen är N då derivatan av detta begrepp är N multipliceras med X upphöjt till n-1, detta upprepas för de andra villkoren i ekvationen och den konstanta termen, är en utan ett X lämnas ut.
- 32Nu har du en funktion som ger dig gradienten av en funktion vid en viss punkt.
- 33Den gradient, i fallet med en förskjutning tid graf som vi talade om, är lika med hastigheten i enheter av avstånd per tidsenhet. Vad som gör detta sätt att beräkna hastigheten speciell är att den tillåter oss att beräkna hastigheten över en oändligt liten tid.
Tips
- Förskjutning är som avstånd men den har en uppsättning riktning, gör denna förskjutning en vektor och påskynda en skalär. Förskjutningen kan vara negativ medan avståndet kommer bara vara positiv.
- Denna Google kommer att bli bättre när jag redigera den.
- Den funktion som beskriver sambandet Y (förskjutning) till X (tid) kan vara riktigt enkelt som [Y = 6x + 3], i detta fall lutning är konstant och det är inte riktigt neccesary att differentiera för att hitta den gradient som naturligtvis är 6.
- Med denna typ av arbete det hjälper verkligen att försöka visualisera problemet och tillämpa matematik när du har bestämt vilken egendom som du behöver för att hitta.
