Resistiva kretsar kan analyseras genom att kombinera nätverken av parallella och motstånd serien till en enda ekvivalent resistans, sedan använda Ohms lag för att hitta den ström eller spänning över den ekvivalenta resistansen. När detta är känd, är det möjligt att arbeta bakåt och använda Ohms lag att beräkna spänningen och strömmen över något motstånd i nätverket.
De ekvationer som behövs för att utföra analysen beskrivs kortfattat tillsammans med arbetat exempel. Referenser citeras eller länkas, men tillräckligt information presenteras här för att tillämpa begrepp utan att behöva referera någon annanstans. Steg-för-steg stil används endast i sektioner där det finns mer än ett steg.
Alla avsiktliga resistanser visas som motstånd (schematiskt, en sick-sack-linje). Anslutningar som visas som linjer antas vara av noll resistans (åtminstone approximativt, i förhållande till de visade motstånd).
Sammanfattningsvis är de grundläggande stegen som visas nedan.
Steg
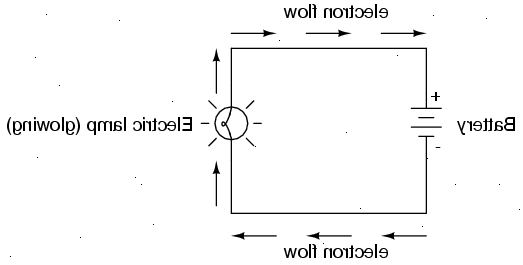
- 1Om det finns mer än 1 motstånd i kretsen, hitta motsvarande motstånd "r" i hela nätverket som visas i "kombinationer av motstånd i serie och parallellt" nedan.
- 2Applicera Ohms lag till detta värde av "r" såsom illustreras i "Ohms lag" nedan.
- 3Om det finns mer än ett motstånd i kretsen, värdet av spänning eller ström beräknas i det föregående steget kan användas i Ohms lag för att hitta spänningen över eller strömmen genom varje annan resistor i nätverket.
Ohms lag
Ohms lag kan skrivas på tre likvärdiga former beroende på vad som löst för:
(1) V = IR
(2) I = V / R
(3) R = V / I
"V" är spänningen över resistansen (den "potentialskillnaden"), "I" är strömmen genom motståndet, och "R" är värdet av motståndet. Om motståndet är ett motstånd (en komponent med ett kalibrerat värde av motstånd) är det vanligtvis märkt med "R" följt av ett nummer, t.ex. "R1", "R105", etc.
Form (1) lätt omvandlas till former (2) eller (3) genom algebraisk manipulation. I vissa fall bokstaven "E" används i stället för "V" (till exempel E = IR), där "E" står för EMF eller "elektromotorisk kraft" som är ett annat namn för spänning.
Form (1) används när strömmen är känd genom ett motstånd med känt värde.
Form (2) används när spänningen är känd över ett motstånd med känt värde.
Form (3) används, förutsatt att motståndet värdet är okänd, men spänningen över den och ström genom den är kända, så att motstånd som skall beräknas.
Standarden () enheter av varje parameter i Ohms lag är:
- Spänningsfall över resistorn "V" är i, förkortat "V". Förkortningen "V" för "volt" är inte att förväxla med spänningen "V" i Ohms lag.
- Nuvarande "Jag" är i ampere, ofta förkortat till "ampere", förkortat "A".
- Resistance "R" är i ohm, ofta representerad av den grekiska symbolen huvudstaden omega (Ω). Bokstaven "K" eller "k" betecknar en multiplikator av "tusen" ohm "M" eller "MEG" betyder multiplikator på en "miljon" ohm. Ofta Ω symbolen inte är skriven efter en multiplikator, exempelvis en 10,000 Ω motstånd är vanligtvis märkt "10K" i stället för "10 K Ω".
Ohms lag gäller varje krets som endast innehåller resistiva element (t.ex. motstånd komponenter, eller om motståndet av ledare såsom kablar eller PC löpare board). Om det finns reaktiva element (induktorer eller kondensatorer) det inte gäller direkt i den form som visas ovan (ekvationen ovan bara innehåller "R", som inte omfattar induktans eller kapacitans). Ohms lag kan användas på resistiva kretsar huruvida den pålagda spänningen eller strömmen är DC (likström), AC (växelström) eller någon slumpvis tidsvarierande signal undersöktes vid varje tidsögonblick. Om den drivande spänning eller ström är sinusformad växelström (t.ex. från en 60 Hz hushåll eluttag), enheterna för spänning och ström är vanligtvis volt eller ampere .
För mer information om Ohms lag, inklusive hur det kan härledas och dess historia, se Wikipedia Ohms lag artikeln.
Exempel: spänningsfall över en tråd
Antag att vi vill hitta spänningsfallet över en vira när en ström av en amp strömmar genom den. Tråden resistans mäter 0,5 Ω. Använda formulär (1) av Ohms lag ovanför hittar vi spänningsfallet över tråden är:
V = IR V> = (1 A) (0,5 Ω) = 0,5 V (det vill säga 1/2 volt)
Om strömmen varit 60 Hz elektrisk hushåll ström av 1 A AC RMS, skulle resultatet ha blivit detsamma, (0,5), men enheterna skulle ha varit "volt växelström RMS".
Motstånd i serie
Den totala end-to-end-motståndet hos en sträng av motstånd anslutna i "serie" (se figur) är helt enkelt summan av alla resistanser. För "n" resistorer märkta R1, R2,..., Rn.
R total = R1 + R2 +... + Rn
Exempel: motstånd i serie
Antag att det finns 3 motstånd kopplade i serie:
R2 = 22 Ohm
Den totala end-to-end motstånd är:
R total = R1 + R2 + R3 = 10 + 22 + 0,5 = 32,5 Ω
Motstånd parallellt
Den totala resistansen över en uppsättning resistorer parallellkopplade (se diagrammet till höger) ges av:
Gemensam notation betyder "parallellt med" är att skriva två parallella snedstreck ("/ /"). Exempelvis kan R1 parallellt med R2 att betecknas som "R1 / / R2". Observera att R1 / / R2 = R2 / / R1. En uppsättning av 3 motstånden R1, R2 och R3 alla samtidigt skulle kunna betecknas "R1 / / R2 / / R3".
Exempel: resistorer parallellt
För 2 motstånd parallellt, R1 = 10 Ω och R2 = 10 Ω (båda samma värde), har vi:
Också anges som "mindre än den minsta" Betyder det totala motståndet alltid kommer att vara mindre än motståndet minsta motståndets i kretsen.
Kombinationer av motstånden i serie och parallellt
Nätverk av kombinationer av serie-och parallellkopplade resistorer kan analyseras genom att kombinera dem till en enda "likvärdig" eller "total" motstånd.
Steg
- 1Generellt kombinera alla parallella motstånd till motsvarande parallella resistanser med "motstånd parallellt" ovan. Observera att om det finns parallella grenar som också innehåller serieelement, måste dessa först kombineras genom att motstånden i den grenen.
- 2Kombinera Seriemotstånd genom att lägga till dem, för att få det totala motståndet av nätet, r totalt.
- 3Använd Ohms lag för att hitta den totala strömmen i nätet för en tillämpad given spänning, eller den totala spänningen över nätet för en tillämpad given ström.
- 4Den totala spänning eller ström beräknas i det föregående steget används för att beräkna spänningar och strömmar i nätverket med hjälp av Ohms lag.
- 5Tillämpa denna ström eller spänning till Ohms lag för att hitta spänningen över eller strömmen genom varje annan resistor i nätverket. Detta är mest kortfattat illustreras med exemplet nedan.
Observera att de 2 första stegen ovan kan behöva tillämpas iterativt för stora nätverk.
Exempel: serie / parallellt nätverk
För det nätverk som visas till höger, först de parallella motstånden kommer att kombineras för att hitta R1 / / R2, då det totala motståndet av nätet (över terminalerna) hittas från:
R Totalt = r3 + r1 / / R2
Antag R3 = 2 Ω, R2 = 10 Ω, R1 = 15 Ω, och ett 12 V batteri används i nätverket så V totalt = 12 volt. Lösa använda stegen ovan har vi:
Spänningen över R3 (betecknad V R3) kan nu beräknas från Ohms lag, eftersom strömmen genom den är känd för att vara 1,5 ampere:
V R3 = (I totalt) (R3) = 1.5 A x 2 Ω = 3 volt
Spänningen över R2 (som är densamma som spänningen över R1) kunde beräknas med hjälp av Ohms lag genom att multiplicera strömmen I = 1,5 ampere gånger den ekvivalenta parallella motståndet R1 / / R2 = 6 Ω, vilket gav 1,5 x 6 = 9 volt, eller skulle kunna beräknas genom att subtrahera spänningen över R3 (V R3, precis beräknats ovan) från den pålagda spänningen på 12 volt, det vill säga 12 volt - 3 volt = 9 volt. När detta är känt strömmen genom R2 (betecknad I R2) kan beräknas från Ohms lag (där spänningen över R2 betecknas med "V R2"):
I R2 = (V R2) / R2 = (9 volt) / (10 Ω) = 0,9 amp
Strömmen genom R1 skulle på liknande sätt hittas med hjälp av Ohms lag genom att dela spänningen över den (9 volt) genom dess motstånd (15 Ω), vilket gav 0,6 ampere genom R1. Observera att strömmen genom R2 (0,9 ampere) plus strömmen genom R1 (0,6 ampere) är lika med den totala strömmen i plintarna på 1,5 ampere.
