Wko

Hur lösa exponenter

Exponenter är ett snabbt sätt att skriva hur många gånger ett nummer (basen) multipliceras med sig själv.
x n = x *... * X (n gånger), här x är basen och n är exponenten.

Steg

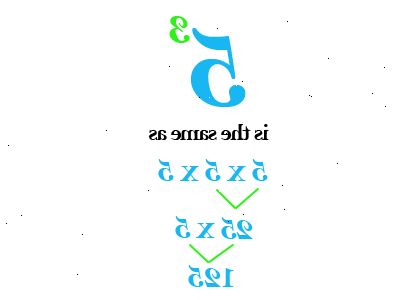
Hur lösa exponenter. Multiplicera basen med sig som dikteras av antalet upphöjd till höger om den (exponent).
Hur lösa exponenter. Multiplicera basen med sig som dikteras av antalet upphöjd till höger om den (exponent).
  1. 1
    Multiplicera basen med sig som dikteras av antalet upphöjd till höger om den (exponent). Till exempel skulle 4 8 vara samma som 4 x 4 x 4 x 4 x 4 x 4 x 4 x 4, eller 4 gånger själv 8 gånger. Detta är lika med 65536.
    • Exponenter är också läsas som "makt." Till exempel, 4 till exponent 8, 4 8 är också "4 upphöjt till 8".
  2. 2
    Observera att denna regel förändras något om exponenten är negativ.
    x-y = 1 / x y
    Så för negativa exponenter bara dividera ett med basen upphöjt till exponenten och lösa som vanligt.
    Ex. 2 -3 = 1/2 3 = 1/8.
    • Ett exempel på en negativ exponent är "det reciproka värdet av ett nummer", som valfritt antal till exponenten -1 (effekt av negativ en) är det reciproka värdet, till exempel: 4 -1 = 1/4 (det reciproka värdet av 4 är en / 4), så "4 upphöjt till -1 är en fjärdedel".
    • Likaså "är trekvart till makt -1 Four Thirds" 3/4 -1 = 4/3 (motsvarigheten till 3/4 är 4/3), så.
  3. 3
    Betrakta en bråkdel som exponent: då nämnaren representerar "roten till bastalet", och nämnaren "höjer basen till en makt", till exempel:
    • Förenkla 2 1/2: Här täljaren "höjer 2 till en 1: a power" som inte har någon effekt alls! Nämnaren 2 betyder "andra roten av två" och så förenkling:
      2 1/2 = sqrt (2) eller ~ 1,414...
      (Notera: symbolen "~" betyder ungefär; också notera: "1.414..." är det irrationella, icke-avslutande och icke-repeterande decimal motsvarighet kvadratroten ur 2, och inse att det "..." betyder "fortsätter-oändligt").
    • Förenkla 27 2/3: Här nämnaren del 3 betyder "en tredjedel roten 27" men då täljaren 2 är kraften på det steget, och tillsammans de betyder:
      27 2/3 = (27 1/3) 2 = 3 2 = 9
      (Observera: förstår att den 3: e roten 27 = 3, dvs: 3x3x3 = 27, slutligen 3 kvadrat ger dig 9).
    • Förenkla 8 4/3: Här nämnaren del 3 betyder "en tredjedel roten 8" men då täljaren 4 är kraften på det steget, och tillsammans de betyder:
      8 4/3 = (8 1/3) 4 = 2 4 = 16
      (Observera: förstår att den 3: e roten av 8 = 2, då är 2 höjs till den 4: e = 16, vilket betyder 2x2x2x2 = 16).
  4. 4
    Lös exponenter av factoring basen med dina multiplikation fakta (utan miniräknare). Använd också de faktorer för att analysera och förstå en exponent, "power" eller "root" och motsatsen uttryck av varje, bland annat med hjälp av det reciproka värdet av exponenten, och vissa symboler, såsom:
    • Tänk reella konstanter a k = b och det motsatta B 1 / k = a. Det är en generell form eller ett mönster.
    • Lös 81 1/2.
      9x9 = 81, så sqrt (81) = 9 eller 9 2 = 81 och så 81 1/2 = 9 81 1/2.
    • Lös 64 1/2. Finns det en perfekt kvadrat? "Ja.":
      Vi har 8x8 = 64, OR 8 2 = 64, så att 64 1/2 = 8 64 1/2
    • Lös 64 1/3. Ofta försöker vi factoring helt:
      64 = 32x2 = (16x2) x2 = (8x2) x2x2 = (4x2) x2x2x2 = 2x2x2x2x2x2. Kan vi göra tre identiska grupper av faktorer? "Ja.":
      Omgruppering (2x2) x (2x2) x (2x2) = 4x4x4 OR 4 3 = 64, så 64 1/3 = 4 64 1/3
    • Lös 64 1/6. Kan vi använda de faktorer? "Ja.":
      64 = 2x2x2x2x2x2. Det är 2 6 = 64, så 64 1/6 = 2 64 1/6.

Tips

  • Alla utom noll till makten av 0 är alltid 1, 4 0 = 1.
    • Base noll till noll exponent, dvs: 0 0 är inte definierat. Datorer eller miniräknare ska returnera fel.
  • "Förenkling" i matematik medel göra de angivna verksamheter för att få den enklaste formen av de berörda uttrycken.
  • Avancerad algebra för imaginära tal, e Aix = cos ax + i sin yxa, där i = sqrt (-1), e är ett irrationellt, fortsätter konstant lika ungefär 2,71828..., och en = en godtycklig konstant. Beviset kan hittas i de flesta böcker om högre matematik.
  • De flesta miniräknare har en knapp som du trycker på för att vara exponenten efter att sätta i basen för att lösa exponenten problem. Det kommer förmodligen märkas ^ eller x ^ y.
  • Du kan skriva exponenter som detta på wiki webbplatser i wiki-kod som liknar HTML: x <sup> y </ sup>, som kommer att producera x y.
  • Valfritt antal upphöjt till 1, den första makten, är det numret i sig, det vill säga: 4 1 = 4. Anm: 1 är identiteten inslag av exponenter. Dessutom är 1 identiteten inslag av multiplikation (1 används som multiplikator) och division (1 används som divisor).
    • Identiteten inslag i ett system eller en grupp av siffror (för en viss verksamhet) ger alltid det ursprungliga antalet själv (sin identitet).
  • 1 till någon exponent är 1 är bara 1 x 1 x 1 x... = 1. Så är 1 n bara en 1 x 1 2 x 1 3 x... x 1 n = 1, "1 till n: te makten är 1". (Sub eller nedsänkt siffror räknar bort de delar av produkten.)

Varningar

  • Öka exponenterna orsakar en produkt magnitud att stiga mycket snabbt, så att även om svaret kan tyckas fel, kan det faktiskt vara rätt. (Du kan kontrollera detta genom att plotta en exponentiell funktion, t.ex.: 2 x om x har ett intervall av värden.)