Hur beräkna det geometriska medelvärdet

Geometriska medelvärdet är ett matematiskt begrepp som är relaterat till, men lätt förväxlas med den mer vanligt förekommande aritmetiska medelvärdet. För att beräkna det geometriska medelvärdet, använda någon av metoderna nedan.

Steg

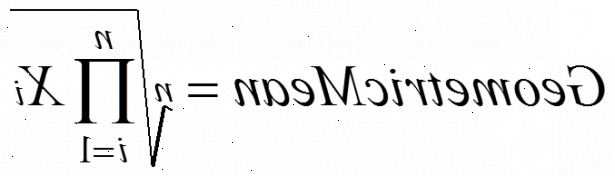
Hur beräkna det geometriska medelvärdet. Hitta de nummer du önskar genomsnittet.

Två siffror: enkel metod

1
Hitta de nummer du önskar genomsnittet.
- Ex. 2 och 32.
2
Multiplicera ihop dem.
- Ex. 2 x 32 = 64.
3
Beräkna kvadratroten av nämnda antal.
- Ex. √ 64 = 8.

Två siffror: detaljerad metod

1
Anslut dina siffror i ekvationen nedan.
Om dina siffror är 10 och 15, till exempel, koppla in 10 för "första #" och 15 för "andra #."
2
Lös för X.
Börja med cross-multipliceringsorgan, vilket innebär att multiplicera tvåsiffriga nummer diagonal till varandra och sedan ställa resultaten på motsatta sidor av ett = tecken. Eftersom X * X är X ^ 2, bör din ekvation ser ut: X ^ 2 = (produkt av dina andra nummer).
För att lösa för X, hitta kvadratroten av din produkt. Om du har tur, kommer resultatet att bli ett heltal. Om inte, kan du ge en decimal svar eller lämna ditt svar i kvadratroten form beroende på vad din instruktör föredrar. Exemplet nedan är förenklad kvadratroten formulär.

Tre eller fler siffror: enkel metod

1
Anslut dina siffror i ekvationen nedan.
Medel = (a ₁ × ₂... a _n) ^{1 / n}
- en ₁ är ditt första numret är en ₂ ditt andra nummer, och så vidare
- n är antalet poster
2
Multiplicera siffrorna (a _1, a _2, osv.) Tillsammans.
3
Beräkna den n: te roten av detta nummer. Detta är det geometriska medelvärdet.

Tre eller fler siffror: detaljerad metod

1
Hitta loggen för varje nummer och tillsätt de logaritmiska värdena tillsammans.
Hitta på LOG-knappen på din miniräknare. När du är redo, typ: (första siffran) LOG + (andra siffran) LOG + (tredje numret) LOG [+ log av ytterligare nummer som behövs] =. Försumma inte att skriva = Eller numret du ser blir loggen för den senaste numret, inte den totala.
- Ex. log 7 + log 9 + log 12 = 2,878521796...
2
Dividera summan av de logaritmiska värdena med antalet värden du lagt till. Om du lagt till stockarna av tre siffror, dividera med tre.
- Ex. 2,878521796 / 3 = 0,959507265...
3
Hitta antilog av ditt resultat. På din räknare, tryck på 2: a funktionen (oftast gul) och sedan logga 2nd> för att aktivera den sekundära funktionen av stocken knappen, eller antilog. Detta resulterande värdet är det geometriska medelvärdet.
- Ex. antilog 0,959507265 = 9,109766916. Därför är det geometriska medelvärdet av 7, 9, och 12 9.12.

Tips

Skillnad mellan aritmetiska och geometriska medelvärdet:
- Om du ville ha det aritmetiska medelvärdet av 3, 4 och 18, till exempel, skulle du lägga 3 + 4 + 18, sedan dividera med 3 eftersom det finns tre siffror. Resultatet skulle bli 25/3 eller ca 8.333..., vilket visar att om du hade tre värden på 8,3333..., skulle det ge samma totala som de individuella värdena 3, 4 och 18. Det aritmetiska medelvärdet svarar på frågan, "Om alla de kvantiteter som hade samma värde, vad skulle det värdet måste vara för att lägga upp till samma totala?"
- Däremot var det geometriska medelvärdet svarar på frågan, "Om alla de kvantiteter hade samma värde, vad skulle det värdet måste vara för att få samma produkt när den multipliceras?" Så för att hitta det geometriska medelvärdet av 3, 4 och 18, skulle vi multiplicerar 3 x 4 x 18. Detta skulle ge oss 216. Vi skulle sedan ta kubikroten (kubikroten eftersom det fanns tre original nummer). Svaret skulle vara 6. Med andra ord, eftersom 6 x 6 x 6 = 3 x 4 x 18, 6 är det geometriska medelvärdet av 3, 4 och 18.
Det geometriska medelvärdet för varje uppsättning siffror är alltid mindre än eller lika med det aritmetiska medelvärdet av det kastet. Se Wikipedia: AM-GM_inequality
Det geometriska medelvärdet gäller endast icke-negativa tal. I ord problem när du använder ett geometriskt medelvärde är lämpligt, kommer det scenario vanligtvis inte vettigt med negativa tal.