Hur att hitta matematiska sannolikheter

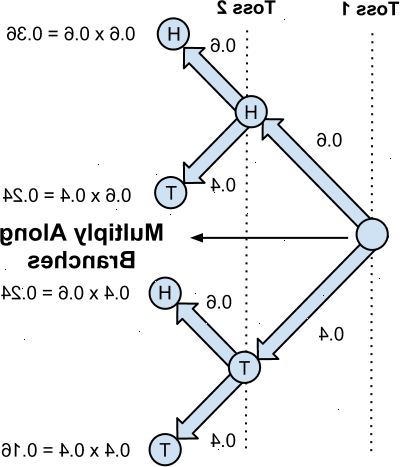
Sannolikheten för en oberoende händelse

1. 1
   Räkna antalet alla särskiljande och lika sannolika utfall av försöket. Låt det vara n.
   
2. 2
   Räkna antalet distinkta utfall som representerar förekomsten av händelsen i fråga. Låt det vara n _e.
   
3. 3
   Beräkna resultatet av uppdelningen N _e / n. Detta är sannolikheten att händelsen.
   
4. 4
   Exempel: "Hitta sannolikheten att få ett jämnt antal efter valsningen en die"
   
   • Experiment: Rolling en rättvis dör
   • Händelse: Att få ett jämnt antal
   • Stegen ovan:
     1. Utmärkande resultat: 1, 2, 3, 4, 5, 6 är alla resultat, deras räkna n = 6
     2. Resultat representerar händelsen: 2, 4, 6 är alla jämna tal du kan få, deras antal n _e = 3
     3. Sannolikhet: P = n _e / n = 3/6 = 0,5 eller 1/2

     Sannolikhet för oberoende händelser inträffar tillsammans / samtidigt

     1. 1
        Hitta den individuella sannolikheten för varje händelse som inträffar av sig själv.
        
     2. 2
        Multiplicera de individuella sannolikheterna att hitta sannolikheten för dem alla händer tillsammans.
        
     3. 3
        Exempel: "En tärning slås, ett mynt kastas, och en spinner med siffrorna 1 till 5 spinns Hitta sannolikheten att få en 3, ett huvud och en 4 på tärningen, mynt och spinner respektive samtidigt.. "
        
        1. Individuella sannolikheter:
           1. Att få en 3 när rullande en die: P ₁ = 1/6 (med metoden ovan)
           2. Att få ett huvud när man singlar slant: P ₂ = 1/2
           3. Att få en 4 när en spinner spinns: P ₃ =: 1/5
        2. Sannolikhet: P = P ₁ * P ₂ * P ₃ = 1/6 * 1/2 * 1/5 = 1/60

        Sannolikhet för beroende händelser

        1. 1
           Beräkna sannolikheten för den första händelsen. I nästan alla fall, det finns en eller flera händelser som andra händelser beroende. Detta bör vara ditt första att beräkna. Det är oberoende av sig själv så det första avsnittet gäller.
           
        2. 2
           Identifiera den förändring som den första händelsen görs på miljön av experimentet. Vanligtvis i dessa situationer, förekomsten av den första händelsen antingen begränsar eller ökar antalet möjliga utfall av försöket.
           
        3. 3
           Beräkna sannolikheten för den andra händelsen (det fall beror omedelbart vid eller följer omedelbart efter den första händelsen) med användning av metoden i det första avsnittet i ljuset av den förändring som avses i 2.
           
        4. 4
           Fortsätta att upprepa steg 2 och 3 för efterföljande händelser, identifiera förändringar som gjorts av de tidigare händelserna därefter beräkna sannolikheten för en ny händelse i ljuset av denna förändring.
           
        5. 5
           Multiplicera alla sannolikheter du beräknade i föregående steg, som kommer att vara sannolikheten för de beroende händelserna helt och hållet.
           
        6. 6
           Exempel: "Det finns en påse med 5 gröna kulor, 2 röda sådana, och 3 blåa Hur stor är chansen att två blå kulor och sedan en röd marmor väljs slumpmässigt ur påsen.?"
           
           1. Första händelse: att välja en blå marmor (den första i de två blå kulor att väljas först)
              1. Distinkt resultaten av experimentet: 5 grön + 2 röd + 3 blå = 10 kulor
              2. Resultat representerar händelsen: 3 blå
              3. P ₁ = 3/10
           2. Förändring görs av händelse 1: antal utfall ändrats till 5 gröna + 2 röd + 2 blå = 9 kulor.
           3. Andra händelse: att välja en blå marmor, med sannolikheten 2 blå kulor / 9 totalt = 2/9
           4. Förändring av händelse 2: antal utfall ändrats till 5 grön + 2 röd + 1 blå = 8 kulor
           5. Tredje händelse: att välja en röd marmor, med sannolikheten 2 röda kulor / 8 totalt = 1/4
           6. Total sannolikhet: P _Totalt = P ₁ * P ₂ * P ₃ = _3/10 * 2/9 * 1/4 = 6/360 = 1/60

           Termer och definitioner

           • Oberoende händelser: är två händelser som inte påverkar varandra. Exempelvis påverkar rullen av ett munstycke inte resultatet av rullen av en annan form eller tossen av ett mynt.
           • Beroende händelser: påverkar varandra. Till exempel, om en kula tas ut ur en påse och ersätts inte, påverkar det chanserna för att en viss marmor skulle dras nästa.
           • Experimentet: är den allmänna ramen inom vilken händelsen skall inträffa. Med andra ord är det den serie av åtgärder som kommer att utföras på miljön vilket leder till förekomsten av händelser. Till exempel, singla slant, rulla en tärning, välja en boll från en säck eller ens köra till en viss stat. Det beror helt på sammanhanget av problemet.
           • Miljön: är den uppsättning av resurser som kommer att användas i försöket. Till exempel, ett munstycke, två mynt, 6 gröna kulor, en van eller ens en motorväg gata. Återigen, det beror på sammanhanget av problemet.

           Tips

           • Var extra noga med att varje ord i problemformuleringen. Se upp för följande ord och förstå deras exakta innebörd i sammanhanget:
             • Och, eller, inte, men
             • Alla för varje, för varje
             • Utom
             • "Minst", "de"
             • "Med", "utan"
             • "Endast om", "om och endast om", "om"
           • Beräkning beroende händelser är lätt trasslat. Det kan vara användbart om du drar någon form av ett diagram för att representera händelseförloppet och effekten var och en gör för miljön av experimentet.