Hur att faktorn andra gradens polynom (andragradsekvationer)

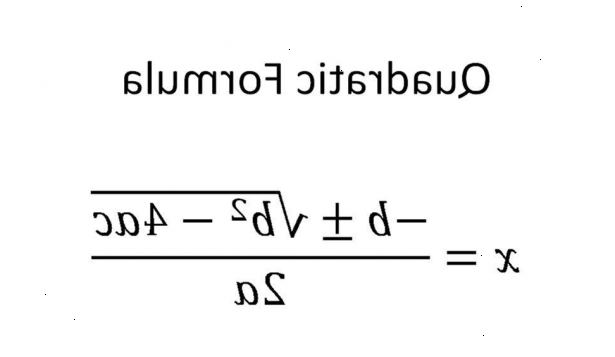
1. 1
   Ställ in ditt uttryck. Beställ siffrorna från högsta till lägsta effekt och sedan faktor ut den största gemensamma faktorn om en sådan finns.
   6 + 6x ² + 13x
   6x ² + 13x + 6
2. 2
   Find the factored formen genom att använda någon av metoderna nedan.
   (2x + 3) (3x + 2)
   
3. 3
   Kontrollera ditt arbete genom att multiplicera de faktorer med metallfolie. Sedan kombinera liknande termer och du är klar!
   (2x + 3) (3x + 2)
   6x ² + 4x + 9x + 6
   6x ² + 13x + 6
   

Trial and error-metoden

Om du har en ganska enkel polynom, kommer du att kunna räkna ut vilka faktorer själv. OBS: Med denna metod kan inte vara så enkelt som när factoring mer komplicerade trinomials.

Exempel: 3x ² + 2x - 8

1. 1
   Lista de faktorer i en term och c sikt.
   a = 3 faktorer: 1 och 3
   c = -8 faktorer: 2 och 4 eller 1 och 8
   
2. 2
   Skriv ner två uppsättningar av parenteser med tomma utrymmen så här:
   (X) (x)
   
3. 3
   Fylla utrymmena framför x: s med ett par möjliga faktorer för ett värde. Det finns bara en möjlighet för vårt exempel:
   ( 3x) ​​( 13x) (x)
   
4. 4
   Fyll i de två utrymmena efter x: s med ett par faktorer för konstanten. Låt oss säga att vi väljer (3x 8) (x 18) (x).
   
5. 5
   Bestäm vilka tecken bör vara mellan X och siffrorna. Här är en guide:
   Om ax ² + bx + c då (x + h) (x + k)
   Om ax ² - bx - c eller ax ² + bx - c därefter (x - h) (x + k)
   Om ax ² - bx + c därefter (x - h) (x - k)
   För vårt exempel 3x ² + 2x - 8 så (x - h) (x + k)
   Vi får gissa så för resten. (3x + 8) (x - 1)
   
6. 6
   Testa ditt val genom att multiplicera (använd folie) de två parenteser tillsammans. Om mitten sikt är inte minst det korrekta värdet (bortsett positiv eller negativ) du har valt fel c faktorer.
   (3x + 8) (x - 1)
   3x ² - 3x + 8x - 8
   3x ² + 5x - 8 ≠ 3x ² + 2x - 8
   
7. 7
   Byt ut dina val om det behövs. I vårt exempel, låt oss försöka 2 och 4 istället för 1 och 8: (3x + 2) (x - 4)
   
   • Nu har vår c termen är en -8.
   • Men vår ute / inne combo är-12x och 2x, vilket inte kommer att kombinera att göra rätt B löptid 2 x.
8. 8
   Omvänd ordning om det är nödvändigt. Låt oss försöka flytta 2 och 4 runt: (3x + 4) (x - 2)
   
   • c sikt är fortfarande okej.
   • Outside / Inside combo är-6x och 4x. Om vi ​​kombinerar dem, får vi ganska nära till 2x vi siktade för --- rätt belopp, fel tecken.
9. 9
   Dubbelkolla dina skyltar vid behov. Vi kommer att hålla sig till samma ordning, men swap som man har subtraktion: (3x - 4) (x + 2)
   
   • c sikt är fortfarande okej.
   • Outside / Inside combo är nu 6x och-4x. Detta kommer att kombineras för att skapa den positiva 2x från det ursprungliga problemet, så det är rätt faktorer.

Nedbrytning metod

Om siffrorna är stora eller är du bara trött av gissningar använda denna metod.

Exempel: 6x ² + 13x + 6

1. 1
   Multiplicera en term (6 i exemplet) av c sikt (även sex i exemplet).
   6 • 6 = 36
   
2. 2
   Hitta två siffror som när den multipliceras lika här numret (36) och lägga till upp till vara den b sikt (13).
   4 • 9 = 36 4 + 9 = 13
   
3. 3
   Ersätt de två siffror du får in detta formulär så k och h (ordningen spelar ingen roll): ax ² + kx + hx + c
   6x ² + 4x + 9x + 6
   
4. 4
   Faktor polynom av gruppering. Organisera ekvationen så att du kan ta ut den största gemensamma faktorn för de två första terminerna och de två sista terminerna. Båda dimensionerande grupper bör vara samma. Lägg GCF: s samman och innesluta dem i parentes bredvid factored gruppen.
   6x ² + 4x + 9x + 6
   2x (3x + 2) + 3 (3x + 2)
   (2x + 3) (3x + 2)
   

Triple play metod

Det är mycket lik den nedbrytning metod, men det är enklare.

Exempel: 8x ² + 10x + 2

1. 1
   Multiplicera en term (åtta i exemplet) av c sikt (två i detta exempel).
   8 • 2 = 16
   
2. 2
   Hitta två tal vars produkt är detta nummer (16) och vars summa är lika med b-sikt (10).
   2 • 8 = 16 8 + 2 = 10
   
3. 3
   Ta dessa två nummer (som vi kommer att kalla h och k) och ersätta dem i detta uttryck:
   (Ax + h) (ax + k)
   en
   (8x + 8) (8x + 2)
   8
   
4. 4
   Titta att se vilken av de två parentes termer i täljaren är jämnt delbart med en {i detta exempel är det (8x + 8)}. Dividera denna term med en och lämna den andra som är.
   (8x + 8) (8x + 2)
   8
   Svar: (x + 1) (8x + 2)
   
5. 5
   Ta GCF (om någon) av endera eller båda parenteser.
   (X + 1) (8x + 2)
   2 (x + 1) (4x + 1)
   

Skillnad av två kvadrater

1. 1
   Faktor ut en GCF om du behöver.
   27x ² - 12
   3 (9x ² - 4 ^för)
   
2. 2
   Bestäm om din ekvation är en skillnad av kvadrater. Den måste ha två termer och du bör kunna ta kvadratroten av termerna jämnt.
   √ (9x ²⁾ = 3x och √ (4) = 2 (notera att vi har lämnat ut minustecknet)
   
3. 3
   Sätt a och c-värden från din ekvation i detta uttryck:
   (√ (a) + √ (c)) (√ (a) - √ (c))
   3 [(√ (9x ²⁾ + √ (4)) (√ (9x ²⁾ - √ (4))]
   3 [(3x + 2) (3x - 2)]
   

Använda den kvadratiska formeln

Om allt annat misslyckas och ekvationen inte kommer faktor jämnt använder kvadratiska formel.
Exempel: x ² + 4x + 1

1. 1
   Anslut motsvarande värden i den kvadratiska formel:
   x =-b ± √ (b ² - 4ac)
   2a
   x = -4 ± √ ^(april 02-04 • 1 • 1)
   2 • 1
   
2. 2
   Lös för x. Du bör få två x-värden.
   x = -4 ± √ (16 - 4)
   2
   x = -4 ± √ (12)
   2
   x = -4 ± √ (4 • 3)
   2
   x = -4 ± 2 √ (3)
   2
   x = -2 ± √ (3)
   x = -2 + √ (3) eller x = -2 - √ (3)
   
3. 3
   Anslut x-värdena (h och k) i detta uttryck: (x - h) (x - k)
   (X - (-2 + √ (3)) (x - (-2 - √ (3))
   (X + 2 + √ (3)) (x + 2 - √ (3))
   

Använda en miniräknare

Dessa riktningar är en TI grafräknare. De är särskilt användbara i standardiserade tester.

1. 1
   Ange din ekvation i [y =]-skärmen.
   y = x ² - x - 2
   
2. 2
   Tryck [graf]. Du bör se en mjuk båge.
   
3. 3
   Leta där ljusbågen skär x-axeln. Dessa är de x-värden.
   (-1, 0), (2, 0)
   x = -1, x = 2
   
   • Om du inte kan identifiera dem genom synen tryck på [2] och därefter [TRACE]. Tryck på [2] eller välj "noll". Skjut markören till vänster om ett skär och tryck [ENTER]. Skjut markören till höger om ett skär och tryck på [ENTER]. Skjut markören så nära som möjligt till den skär och tryck på [ENTER]. Räknaren hittar x värdet. Gör detta för den andra skär också.
4. 4
   Anslut x-värdena (h och k) i detta uttryck: (x - h) (x - k)
   (X - (-1)) (x - 2)
   (X + 1) (x + (-2)) stort plus lägga till den gemensamma faktorn